|
|
LO3
|
02.02.2012 - Jakub Łopuszański
|
29.01.2010
Dzisiaj na zajęciach wróciliśmy do problemu wyszukiwania wzorca, tym razem poznając pewne bardzo dobre w praktyce algorytmy oraz drogę rozumowania potrzebną do ich wymyślenia. Najpierw zauważyliśmy, że porównywanie dwóch dużych obiektów, można rozpocząć od porównania wartości ich funkcji hashujących. Powiedzieliśmy sobie, że funkcje hashujące występują w informatyce w dwóch kontekstach znaczeniowych:
|
11.12.2009
Przypomnieliśmy sobie co to jest automat skończony oraz w jaki sposób można automat skończony może pomóc w znajdowaniu wystąpień wzorca.
Dla wzorca 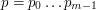 , automat taki ma , automat taki ma 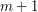 stanów stanów 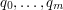 . .
|
04.12.2009
Poznaliśmy pojęcie automatu skończonego, czyli czegoś co składa się z:
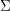 , czyli alfabetu, czyli skończonego zbioru znaczków jakie mogą się pojawić na drodze robaczka , czyli alfabetu, czyli skończonego zbioru znaczków jakie mogą się pojawić na drodze robaczka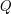 , czyli stanów, czyli skończonego zbioru pewnych abstrakcyjnych konfiguracji pamięci robaczka , czyli stanów, czyli skończonego zbioru pewnych abstrakcyjnych konfiguracji pamięci robaczka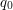 , czyli stanu początkowego, , czyli stanu początkowego, 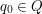 z jakim rodzi się robaczek z jakim rodzi się robaczek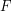 , czyli stanów akceptujących, , czyli stanów akceptujących, 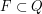 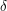 , czyli funkcji przejścia, , czyli funkcji przejścia, 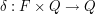 , opisującej proces kognitywny robaczka, czyli w jaki sposób życie wpływa na jego wi , opisującej proces kognitywny robaczka, czyli w jaki sposób życie wpływa na jego wi
|
27.11.2009
Analizując złożoność sita Erastotenesa, natrafiliśmy na dość częstego bohatera: liczby harmoniczne:
Powiedzieliśmy sobie, że zachodzi 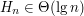 , co da się pokazać prosto dla n będących potęgami dwójki, a następnie dla pozostałych korzystając z tego że 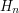 jest monotoniczną funkcją  :
|
20.11.2009
Omówiliśmy sobie Algorytm Euklidesa i parę jego zastosowań.
Polecam gorąco artykuł Damiana Rusaka.
|
13.11.2009
Na zajęciach poznaliśmy też inną struktruę danych, która posiada "explicit layout", jaką jest union-find, zaimplementowany jako pojedyncza tablica.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| int u[N];
int find(int x);
bool unite(int x,int y){
x=find(x);
y=find(y);
if(x==y)return false;
if(u[x]<u[y]){
u[y]=x;
}else if(u[y]<u[x]){
u[x]=y;
}else{
u[x]=y;
--u[y];
}
return true;
}
memset(u,-1,sizeof(u)); |
|
13.11.2009
Dzisiaj na zajęciach opowiedzieliśmy sobie o tym jak zadbać o porządek w kopcu i jak zorganizować sobie strukturę danych w pamięci, aby nie potrzebować wskaźników.
Idea była taka, żeby trzymać wszystko w tablicy:
1
2
3
| const int N=1000;
typedef int T;
T heap[N+1]; |
i ponumerować wierzchołki drzewa z góry na dół od lewej do prawej, począwszy od 1 a na N skończywszy.
Tu może dygresja, żeby pamiętać o tym, iż albo tablica musi mieć o jeden element więcej, albo (jak komuś żal RAMu) należy przesunąć wskaźnik o jeden.
|
11.11.2009
Jednym z trudnych do napisania samemu algorytmów dostępnych w STLu, jest nth_element.
Funkcja z grubsza służy do tego, aby wyszukać k-ty co do wielkości element w podanej tablicy i o tym problemie traktuje niniejszy artykulik.
Zastanówmy się, jak znaleźć ów k-ty element bez korzystania z tej funkcji?
Pomysł 1. sort
Pomysł, który wielu osobom się narzuca, to posortować tablicę i zwrócić jej (n-k)-ty element. Rozwiązanie proste i poprawne, ale o złożoności 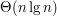 , gdzie n to rozmiar tablicy. , gdzie n to rozmiar tablicy.
|
10.11.2009
Z pewnych względów nie mogłem odpowiedzieć na to pytanie przed CEPCem, ale teraz postaram się zrewanżować.
W niektórych zadaniach chcielibyśmy przyporządkować napisom jakieś obiekty. Czyli chcielibyśmy mieć coś co w STLu nazwalibyśmy map<string,T> gdzie T to typ obiektów jakie chcemy przyporządkować stringom.
|
10.11.2009
Graf, to pojęcie, które jest fundamentalne dla zrozumienia większości olimpijskich problemów i ich rozwiązań. Definicję na pewno znajdziecie w sieci, a większość opracowań zadań używa go bez zbędnych wyjaśnień.
|
10.11.2009
Graf, to pojęcie, które jest fundamentalne dla wymyślenia rozwiązania i zaimplementowania większości olimpijskich zadań.
Jak wiemy z części teoretycznej graf powinien mieć zbiór wierzchołków i zbiór krawędzi. W praktyce jednak, przyjmujemy, że wierzchołki nazywają się od 0 do n-1, i nie musimy nigdzie pamiętać ich zbioru, a jedynie pamiętać, że jest ich n.
|
10.11.2009
Przyjdzie Wam zapewne nie raz startować w zawodach o formule "ACMowej", np. w Dolnośląskich Zawodach w Programowaniu Zespołowym. W najbliższy weekend, odbywają się na Uniwersytecie Wrocławskim najbardziej prestiżowe zawody w tej części Europy, czyli właśnie ACM ICPC CEPC. Parę osób od nas zostało zaproszonych poza konkursem, aby poczuć ducha tej imprezy.
|
|
|