Element k-ty co do wielkości
11.11.2009
 Jednym z trudnych do napisania samemu algorytmów dostępnych w STLu, jest nth_element. Funkcja z grubsza służy do tego, aby wyszukać k-ty co do wielkości element w podanej tablicy i o tym problemie traktuje niniejszy artykulik. Zastanówmy się, jak znaleźć ów k-ty element bez korzystania z tej funkcji? Pomysł 1. sort
Pomysł, który wielu osobom się narzuca, to posortować tablicę i zwrócić jej (n-k)-ty element. Rozwiązanie proste i poprawne, ale o złożoności Pomysł 2. k akumulatorówKolejny pomysł to pewna adaptacja algorytmu na znajdowanie maximum. W owym algorytmie używamy jednego akumulatora, w którym staramy się pamiętać największą liczbę z dotychczas przetworzonych. Modyfikacja polega na tym, by takich akumulatorów mieć nie jeden tylko k, tak aby i-ty z nich przechowywał i-ty co do wielkości element z przetworzonej części tablicy. W zależności od tego jak zorganizujemy sobie owe k akumulatorów i aktualizowanie ich możemy uzyskać bardzo różne algorytmy. Pomysł 2.1. k akumulatorów jako tablicaByć może najprostszym rozwiązaniem jest trzymać akumulatory w k-elementowej tablicy i przetwarzając kolejną daną, porównywać ją z kolejnymi akumulatorami, aż znajdziemy pozycję, gdzie należałoby wstawić ów element. Jednocześnie z szukaniem odpowiedniego miejsca, można już sobie przesuwać akumulatory o jedną pozycję. Ten algorytm w gruncie rzeczy bardzo przypomina InsertionSort, w którym sortowanie polega na tym, że każdy kolejny element próbujemy wstawić na odpowiednie miejsce wśród już posortowanych.
Złożoność tego pomysłu to Pomysł 2.1.2. binary search
Jak to zwykle bywa, gdy mamy problem ze znalezieniem odpowiedniego miejsca w posortowanej tablicy, z pomocą przychodzi nam wyszukiwanie binarne.
Odpowiednie miejsce wśród akumulatorów możemy więc znaleźć w czasie Pomysł 2.2. akumulatory w drzewku
Jak to zwykle bywa, gdy mamy problem ze wstawianiem do posortowanego zbioru, z pomocą przychodzą nam drzewka zrównoważone. Warto znać szablon set Pomysł 2.3. akumulatory w kopcu
W poprzednim rozwiązaniu użyliśmy .r_begin i .erase, aby usunąć najmniejszy akumulator, a ostateczny wynik znajdował się w .back().
Jak to zwykle bywa, gdy wcale nie interesuje nas porządek
między wszystkimi elementami, a jedynie który z nich jest najmniejszy, z pomocą przychodzi nam priority_queue
Domyślnie priority_queue potrafi nam wskazać największy element. Jeśli potrzebujemy zachowania odwrotnego, mamy dwie opcje. Pierwsza, bardzo popularna w warunkach stresu, to przemnożenie wszystkiego przez -1. Ma to tę wadę, że trzeba pamiętać o tym zarówno przy wkładaniu jak i wyciąganiu, oraz niektóre liczby przemnożone przez -1 potrafią zrobić RunTimeError (zagadka: które?). Nieco bardziej elegancko, jest skorzystać z tego, że konstruktor klasy priority_queue, pozwala nam podać obiekt (funktor) używany do porównywania. STL predefiniuje kilka bardzo użytecznych funktorów, np. greater
Używając kopca, push(), pop(), oraz .top() dostajemy całkiem zwięzły algorytm, potrzebujący Pomysł 3. skoro nie Insert,to może BubbleSort?
Wiadomo, że podczas pierwszej iteracji algorytmu BubbleSort maksimum tablicy wybombelkuje na powierzchnię.
Podobnie po k iteracjach BubbleSorta, k największych elementów powinno już znaleźć się na k największych pozycjach w tablicy.
Możemy wtedy przerwać i dostajemy algorytm o złożoności Pomysł 3. no to może SelectSort
Aby znaleźć k-ty co do wielkości element, możemy po prostu k razy znaleźć i usunąć maksimum. Jak się nad tym zastanowić, to jest to dokładnie to co robi algorytm SelectSort w ciągu pierwszych k iteracji. Ponownie dostajemy algorytm o złożoności Pomysł 3.1. do szukania maksimum służy kopiec!Po poprzednim pomyśle, trudno oprzeć się kolejnemu: skoro jedyne co chcemy zrobić to k razy znaleźć maksimum, czemuż nie użyć do tego kopca? Wystarczy zbudować z całej tablicy kopiec, a następnie k razy wyciągnąć z niego maksimum.
Warto wiedzieć, że konstruktorowi priority_queue, można podać zakres (zbiór elementów), którymi ma zostać wypełniony.
Co ciekawsze, o ile wsadzenie n elementów do kopca, jeden po drugim trwa Tak naprawdę to to co robimy to pierwszych k iteracji algorytmu HeapSort. Pomysł 4. no to teraz może quicksort?Jak widać na poprzednich przykładach, często da się przyciąć jakiś znany algorytm sortowania, tak aby rozwiązywał nasz problem. Widzieliśmy to już dla InsertionSort, SelectSort, BubbleSort, HeapSort, pora więc na QuickSort. W algorytmie QuickSort, kluczową operacją jest partition. Swoją drogą jest ona dostępna w STLu. Dzieli ona tablicę na dwa kawałki tak, aby w jednym były elementy duże a w drugim małe. Im sprytniej zaimplementowana, tym większa szansa, że oba kawałki są zbliżonych rozmiarów. Zauważmy, że znając rozmiary kawałków możemy bez trudu ustalić, w którym z nich znajduje się k-ty co do wielkości element.
Nie trudno się domyśleć, że jeśli partition faktycznie zawsze połowiłoby zbiór elementów na pół, a my zawsze schodzilibyśmy rekurencyjnie tylko do jednego z tych dwóch fragmentów, to złożoność otrzymalibyśmy Pozostaje tylko jeden szkopuł -- jak podzielić zbiór na pół. Im dłużej nad tym się myśli, tym bardziej widać, że jest to w gruncie rzeczy równie trudne, jak znalezienie n/2-go co do wielkości elementu, a więc zredukowaliśmy problem do niego samego i to w dość mało przydatny sposób. Na szczęście podobnie jak to ma miejsce z analizą złożoności QuickSort, podobnie i tutaj, wcale nie musimy się upierać, by partition dzieliło zbiór zawsze idealnie na pół. Po pierwsze, nie musi tego robić zawsze -- wystarczy, że raz na parę razy mu się to udaje. Po drugie, nie musi być idealnie na pół -- wystarczy by jedna część nie była bardziej niż parę razy większa od drugiej. Powyższe zrelaksowane założenia całkiem dobrze spełnia partition używająca jako pivotu losowo wybranego elementu. Śmiało można powiedzieć, że z prawdopodobieństwem 50% zapewnia, że żadna z części nie jest ponad 3 razy większa od drugiej. Pomysł 4.1. deterministyczny partitionWiele osób krzywi się na słowo "losowy", a jeszcze więcej na "Nierówność Chernoffa", więc algorytmy zrandomizowane, często próbuje się poddać tak zwanej derandomizacji. Chodzi o to, że jeśli już wiemy, że coś da się zrobić używając generatora liczb losowych, to zastanawiamy się, czy dałoby radę uzyskać zbliżony efekt używając jak najmniej losowych bitów, najlepiej nie używając ich wcale. Chcemy wymyślić algorytm, który dla zadanej tablicy podzieli ją na dwie mniejsze, o porównywalnych rozmiarach. Porównywalnych, tzn. że będzie istniała taka stała C>1, że żadna z nich nie będzie ponad C razy większa od drugiej. Zauważmy, że problem ten jest w pewnym sensie równoważny znalezieniu czegoś co jest w miarę po środku, czyli właśnie pivota, który dałby nam odpowiedni podział. Wiele osób wierzy, że takim pivotem jest np. średnia arytmetyczna maksimum i minimum z tablicy. Rzecz jasna nie jest to prawdą. Nie mniej pomysł jest całkiem dobry w praktyce, bo po pierwsze często dane są w miarę równomiernie rozłożone, a po drugie nawet jeśli nie są, to integer ma tylko 32 bity, więc algorytm, który za każdym razem zmniejsza rozpiętość między minimum a maksimum o połowę, wykona tylko co najwyżej 32 wywołania rekurencyjne. Jeśli kogoś zadowala rozwiązanie bazujące na tym, że integer ma tylko x bitów, to niedobrze. Po pierwsze należy pamiętać, że chociaż głównie sortujemy liczby, to wcale nie jest powiedziane, że tak być musi, poza tym mogą to być double. Po drugie, jeśli ktoś jest takim fanatykiem patrzenia na wszystko poprzez pryzmat O(1)=O(2^32), to może w ogóle posortować najpierw tablicę RadixSortem w czasie O(n) i na tym poprzestać.
Wróćmy więc do problemu szukania czegoś co będzie na prawdę w miarę po środku. Być może kojarzycie metodę turniejową znajdowania maksimum zbioru. Polega na tym, że najpierw dzielimy zbiór na małe grupki (pary) i rozstrzygamy w ich obrębie kto jest maksimum, a potem rekurencyjnie szukamy maksimum wśród tych zwycięzców. Algorytm ten działa w
Pojedynki w parach, były spoko, jeśli potrzebowaliśmy rozstrzygnąć kto jest większy. Jeśli jednak chcemy szukać kogoś kto jest po środku, to będziemy potrzebować 3 elementy.
Podzielmy więc zawodników na 3osobowe grupki i wśród każdej grupki znajdźmy tego środkowego.
Mając tę reprezentację przeciętniaków, możemy rekurencyjnie postąpić z nimi. Jest ich 3 razy mniej, więc algorytm znajdzie nam super-przeciętniaka w czasie Czy super-przeciętniak faktycznie jest super-przeciętny? Co o nim wiemy? Może popatrzmy na analogie do algorytmu na znajdowanie maksimum. Skąd wiemy, że zwycięzca turnieju faktycznie jest najlepszy? Bo wiemy, że obaj finaliści pochodzili z pewnych turniejów, w których pozostawili po sobie całą masę pokonanych.
Podobnie jest z naszym super-przeciętniakiem. Spróbujmy przeanalizować od ilu osób jest lepszy.
Wiemy, że w ostatniej rundzie okazał się lepszy od jednej osoby.
Ta osoba dostała się do ostatniej rundy nie bez powodu.
Mianowicie, aby dostać się do ostatniej rundy, trzeba było w przedostatniej rundzie pozostawić po sobie jednego pokonanego.
Myślę, że warto to sobie chociaż raz narysować i przekontemplować. Wyobrazić sobie drzewko, którego każdy poziom to inna runda zawodów (korzeń to ostatnia runda), a w każdym węźle wpisane jest imię tego kto okazał się średni i awansował wyżej. Osoba wpisana w korzeniu to właśnie super-średniak.
Jest ona na pewno nie gorsza, od osób wpisanych w dwóch spośród trzech dzieci korzenia (jedną z nich jest przecież ona sama, a druga to ta co przegrała w finale). Podobnie każda z tych dwóch osób, jest nie mniejsza od pewnych dwóch swoich dzieci w drzewie. Drzewo ma
No dobra, czyli znaleźliśmy coś o czym wiemy, że może po środku nie jest, ale istnieje co najmniej
Coś zrobiliśmy źle. Pierwsze na co warto zwrócić uwagę przy zetknięciu z porażką, to czy na pewno w naszym algorytmie nie pojawiają się jakieś magiczne stałe mające poważny wpływ na wynik. Ewidentnie taką magiczną stałą jest 3. Zamieńmy to na nieparzysty parametr P. Mamy zatem grupki P zawodników, z których wybieramy tego środkowego. Turniej ma zatem OK, skopiowaliśmy pomysł z algorytmu na szukanie maksimum, zachowując rekurencyjną budowę algorytmu, ale chyba ta nasza rekurencja nie jest "aż taka rekurencyjna" jak być powinna i może to dlatego nie zadziałało. Oto inna, "bardzo rekursywna" propozycja która znajdzie podział idealnie na pół, a dokładniej, wskaże medianę zbioru. Mediana to element, który jest "po środku" gdyby je wszystkie posortować. Podobnie jak poprzednio, dzielimy na grupki 3osobowe i wybieramy środkowe elementy z każdej z nich. Następnie rekurencyjnie szukamy mediany wśród nich. Podkreślę, że chodzi tu o wywołanie całego algorytmu od początku do końca dla tych n/3 elementów. Kiedy znamy już medianę, to wiemy, że jest ona nie mniejsza od n/6 elementów "środkowych", a także od kolejnych n/6 elementów "minimalnych", z którymi owe "środkowe" wygrały. Zatem znaleziona póki co osoba jest nie mniejsza od n/3 elementów, oraz (symetrycznie) nie większa od n/3 elementów. Jest więc w miarę w środku! No dobra, ale na razie pokazaliśmy tylko jak mając czarną skrzynkę, która potrafi znaleźć medianę, znaleźć coś co jest w "miarę w środku". Moim zdaniem to raczej porażka a nie sukces. To co musimy pokazać, to jak znaleźć prawdziwą medianę tego dużego zbioru. Na szczęście to co już mamy to element, który potrafi podzielić zbiór na dwa prawie równe kawałki. A zatem mediana musi się znajdować w jednym z nich (w tym ciut większym) i możemy w niej rekurencyjnie szukać. To się robi co raz bardziej pogmatwane, więc opiszę to krok po kroku w pseudokodzie
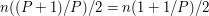 . .
Gdybyśmy podstawili P=3, to oznaczałoby to jedno wywołanie dla tablicy o rozmiarze n/3, a drugie dla tablicy o rozmiarze n2/3.
Nie trzeba chyba nikomu tłumaczyć, że to nie da algorytmu liniowego, bo
Zauważmy jednak, że dla większych P jest nieco lepiej.
Jeśli do Tak o to w bólach doszliśmy do algorytmu Magicznych Piątek.
(2 ocen) |
||||||||||||
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


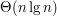 , gdzie n to rozmiar tablicy.
, gdzie n to rozmiar tablicy.
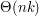 , co widać np. dla ciągów monotonicznych. Po pierwsze ciężko idzie znaleźć miejsce wstawiania, po drugie długo trwa przesuwanie.
, co widać np. dla ciągów monotonicznych. Po pierwsze ciężko idzie znaleźć miejsce wstawiania, po drugie długo trwa przesuwanie.
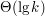 .
Warto znać funkcje lower_bound, oraz copy, dostępne w STLowym pakiecie algorithms.
Nadal jednak mamy problem z przesuwaniem.
.
Warto znać funkcje lower_bound, oraz copy, dostępne w STLowym pakiecie algorithms.
Nadal jednak mamy problem z przesuwaniem.
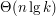 , używa jednak sporo pamięci i strasznie po niej bryka.
, używa jednak sporo pamięci i strasznie po niej bryka.
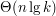 czasu, ale znacznie rozsądniej posługujący się pamięcią, bo do przechowywania akumulatorów używać będzie vector'a, a więc spójnego obszaru pamięci, a nie plątaniny powiązanych ze sobą obszarków jak to robi set.
czasu, ale znacznie rozsądniej posługujący się pamięcią, bo do przechowywania akumulatorów używać będzie vector'a, a więc spójnego obszaru pamięci, a nie plątaniny powiązanych ze sobą obszarków jak to robi set.
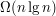 o tyle zainicjalizowanie go od razu n elementami trwa tylko
o tyle zainicjalizowanie go od razu n elementami trwa tylko 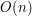 . Oznacza to, że właśnie wymyśliliśmy algorytm o złożoności
. Oznacza to, że właśnie wymyśliliśmy algorytm o złożoności 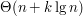 .
.
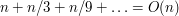 .
.
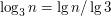 poziomów, a na każdym kolejnym jest dwa razy więcej osób, o których możemy powiedzieć, że są na pewno nie większe niż super-średniak.
Czyli wśród liści jest ich aż
poziomów, a na każdym kolejnym jest dwa razy więcej osób, o których możemy powiedzieć, że są na pewno nie większe niż super-średniak.
Czyli wśród liści jest ich aż 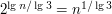 .
.
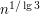 mniejszych elementów od tego czegoś, a także (poprzez symetrię) tyle samo większych. To trochę nie to o co nam chodziło, bo potrzebujemy czegoś co jest
mniejszych elementów od tego czegoś, a także (poprzez symetrię) tyle samo większych. To trochę nie to o co nam chodziło, bo potrzebujemy czegoś co jest 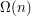 .
.
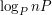 rund, a co za tym idzie super-średniak będzie nie mniejszy od
rund, a co za tym idzie super-średniak będzie nie mniejszy od 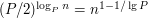 elementów. Ten wzór się nieco nie zgadza z tym dla
elementów. Ten wzór się nieco nie zgadza z tym dla 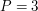 , bo zaokrągliłem
, bo zaokrągliłem 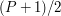 do
do 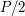 , żeby było prościej dla dużych P. Wygląda na to, że dla żadnego stałego P, nie będzie dobrze, a dla niestałych P, będziemy mieć spory problem ze znalezieniem środkowego elementu.
, żeby było prościej dla dużych P. Wygląda na to, że dla żadnego stałego P, nie będzie dobrze, a dla niestałych P, będziemy mieć spory problem ze znalezieniem środkowego elementu.
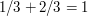 i w zasadzie nie bardzo widać byśmy cokolwiek zredukowali.
i w zasadzie nie bardzo widać byśmy cokolwiek zredukowali.
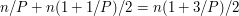 podstawimy na przykład P=5, to otrzymamy
podstawimy na przykład P=5, to otrzymamy 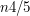 , a więc istotnie mniej niż n.
, a więc istotnie mniej niż n.


