Wyszukiwanie wzorca
11.12.2009
  Przypomnieliśmy sobie co to jest automat skończony oraz w jaki sposób można automat skończony może pomóc w znajdowaniu wystąpień wzorca.
Dla wzorca
Pokazaliśmy sobie, że dla stanu
Powiedzieliśmy sobie, że dla ustalonego
Ustaliliśmy, że taka bezpośrednia implementacja wymagałaby
Pokazaliśmy sobie, że znalezienie Stwierdziliśmy, że możemy w razie potrzeby zmniejszyć zużycie pamięci kosztem czasu działania wyszukiwania wzorca. Np. można myśleć o tym wszystkim na poziomie poszczególnych bitów zamiast bajtów i dzięki temu mieć tablicę o wielkości m*8*2, zamiast m*256, ale koszt jest taki, że algorytm będzie działał 8 razy wolniej. Pod koniec zajęć doszliśmy do rozwiązania, które stara się symulować automat skończony nie pamiętając go. Podczas zabawy w konstruowanie automatu, odkryliśmy przecież, że w nim większość krawędzi jest skopiowana z innego miejsca. Trzymanie kopii informacji jest z reguły symptomem, że coś jest bardzo źle. Warto się zastanowić jak usunąć tego typu redundancję i tym samym skompresować dane.
Ciekawym rozwiązaniem, które przyszło mi właśnie do głowy jest aby automat reprezentować nie jako tablicę tylko jako obiekt.
Tzn zamiast mieć tablicę
Jak widać do poprawnego działania tej funkcji potrzebna jest "tylko" tablica PI. To co jest fajne, to że tablicę PI można zbudować używając funkcji next:
Zauważmy, że do wyliczenia wartości PI[k], musimy wywołać funkcję next, która może potrzebować użyć tablicy PI. Jednak będzie potrzebować dostępu do komórki o numerze mniejszym niż Na sam koniec powiedzieliśmy sobie, że powyższy algorytm jest dobrym przykładem na algorytm dynamiczny, oraz na algorytm o linijowej zamortyzowanej złożoności.
Dynamiczny, to znaczy, że wylicza poprawne wyniki dla większych danych w oparciu na spamiętane wcześniej poprawne wyniki dla mniejszych danych. Słowo "dynamiczny" bierze się stąd, że tego typu algorytmom łatwo w locie powiedzieć, że chcemy wyszukać jednak nieco dłuższy wzorzec. Np. ktoś wpisuje szukany wzorzec literka po literce, a my możemy na bieżąco, czyli dynamicznie aktualizować tablicę Analiza zamortyzowanego kosztu, polega na tym, że algorytm stara się zakumulować trochę niewykorzystanego czasu w "skarbonce", aby móc go potem wykorzystać. W przykładzie podanym na zajęciach, widzieliśmy, że gdyby algorytm wyszukiwania wzorca deponował w skarpecie jedną jednostkę czasu ilekroć wykonuje inkrementację, to mógłby wtedy zapłacić tymi odłożonymi zasobami, za wykonywanie zmniejszania zmiennej w pętli while. Czasem jednak analiza jest nieco bardziej skomplikowana, bo nie widać na pierwszy rzut oka, z jaką zmienną powiązać stan konta. Przykładowo napisany powyżej w pseudokodzie algorytm budowania tablicy PI, ma zamortyzowany czas działania liniowy względem rozmiaru wzorca, a jednak pokazanie tego wymaga nieco więcej finezji.
Powiedzieliśmy sobie wreszcie, że algorytm ten można poprawić tak, aby dawał gwarancję maksymalnego czasu spędzanego na pojedynczą literkę, czyli "zdeamortyzować" go. To będzie na następnych zajęciach.
Wiemy też, że w bibliotece standardowej mamy dostępne strstr, które wyszukuje wzorzec w czasie |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


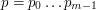 , automat taki ma
, automat taki ma 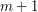 stanów
stanów 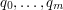 .
.
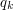 dla
dla 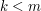 krawędź z literką
krawędź z literką 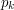 idzie zawsze do stanu
idzie zawsze do stanu 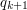 .
Na przykład ze stanu startowego
.
Na przykład ze stanu startowego 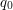 , krawędź z literką
, krawędź z literką 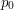 prowadzi do stanu
prowadzi do stanu 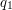 .
Pokazaliśmy także, że inne krawędzie wychodzące z
.
Pokazaliśmy także, że inne krawędzie wychodzące z ![$ q_{\Pi[k]} $](/files/tex/ee960fab19d9115535ecb413661729b79aa0c253.png) .
Podobnie jest dla stanu
.
Podobnie jest dla stanu 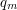 , tyle, że z niego nie wychodzi żadna krawędź w przód.
, tyle, że z niego nie wychodzi żadna krawędź w przód.
 całkiem łatwo znaleźć
całkiem łatwo znaleźć ![$ \Pi[k] $](/files/tex/40a866dec5e112f02936da187fa93574f51d4717.png) . Przypomnijmy sobie, że
. Przypomnijmy sobie, że  o długości
o długości 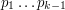 i zobaczyć w jakim stanie się zatrzyma.
i zobaczyć w jakim stanie się zatrzyma.
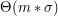 komórek pamięci, gdzie
komórek pamięci, gdzie  to liczba liter w alfabecie, czyli na nasz użytek 256. A także, że konstrukcja automatu wymagałaby czasu
to liczba liter w alfabecie, czyli na nasz użytek 256. A także, że konstrukcja automatu wymagałaby czasu 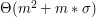 . Pierwszy składnik sumy wynika z naiwnego podejścia do wyszukiwania
. Pierwszy składnik sumy wynika z naiwnego podejścia do wyszukiwania 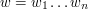 trwa
trwa 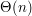
![$ \Pi[k+1] $](/files/tex/56618a9c5f099f7cb16aa34043fe907c68b0bbee.png) można sobie znacząco uprościć, jeśli znaleźliśmy w poprzednim kroku
można sobie znacząco uprościć, jeśli znaleźliśmy w poprzednim kroku ![$ next[m+1][\sigma] $](/files/tex/46fd8bb056d63d67dd5b65a0219e702165503e6b.png) .
.
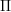 .
.
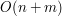 , jednak niekoniecznie musi używać tego samego algorytmu. O innych liniowych algorytmach, oraz algorytmach które starają się zbliżyć do
, jednak niekoniecznie musi używać tego samego algorytmu. O innych liniowych algorytmach, oraz algorytmach które starają się zbliżyć do 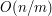 opowiemy sobie na następnych zajęciach.
opowiemy sobie na następnych zajęciach.


