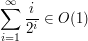Kopiec
13.11.2009
 Dzisiaj na zajęciach opowiedzieliśmy sobie o tym jak zadbać o porządek w kopcu i jak zorganizować sobie strukturę danych w pamięci, aby nie potrzebować wskaźników. Idea była taka, żeby trzymać wszystko w tablicy:
Taka numeracja elementów, pozwala dość łatwo znaleźć ojca, lewe i prawe dziecko. Spróbujcie sami.
Bałagan w kopcu naprawiamy w górę bądź w dół, w zależności od tego, co popsuliśmy. Jeśli zmieniliśmy wartość przechowywaną w danym węźle na mniejszą, to powinniśmy ją spróbować zepchnąć w stronę liści. Jeśli na większą, to powinniśmy popchnąć ją w górę. Jeśli nie jesteśmy pewni to ... możemy spróbować zrobić jedno i drugie. Z reguły jednak wiemy co się stało. Jeśli gmeraliśmy przy czubku, to pewnie zmniejszyliśmy wartość. Jeśli gmeraliśmy przy liściach, to pewnie zwiększyliśmy. Po środku raczej się nie gmera, chyba, że chcemy zmodyfikować przechowywaną wartość. Implementując samemu kopiec, powinniśmy zatem zdefiniować funkcje bubble_up i bubble_down i zadbać o to by robiły to co trzeba. Na zajęciach operację .pop() wyraziliśmy w taki sposób, że najpierw spychamy "dziurę" na dół, a potem w miejsce dziury wsadzamy ostatni element kopca i bąbelkujemy w górę. Alternatywnie można najpierw wsadzić ów ostatni element na sam szczyt, a potem wykonać bubble_down. Są jednak ludzie, którzy wierzą, że wersja z dziurą jest bardziej wydajna:
Na zajęciach omówiliśmy też funkcję make_heap, która potrafi zbudować poprawny kopiec w czasie O(n). Przy okazji zetknęliśmy się po raz kolejny z faktem, że
Powiedzieliśmy sobie też, że w STLu, kopiec realizowany jest jako priority_queue, i o ile nie wyspecyfikujemy inaczej, jako kontenera używa vector'a, a do porównania użyje operatora <. To o czym sobie nie powiedzieliśmy, to, że są sytuacje, w których STLowa implementacja może nam nie wystarczać i napisanie kopca samemu może się przydać. Główny mankament (zaleta?) priority_queue to niemożność dostania się bezpośrednio do jakiegoś elementu, po to by zmienić jego priorytet. Obchodzi się to często poprzez dodawanie tego samego elementu raz jeszcze z innym priorytetem i usuwając jego stare kopie, gdy tylko wypłyną na wierzch i zostaną zwrócone przez .top(). To rozwiązanie często wystarcza i wiele osób tak właśnie implementuje np. algorytm Dijkstry. Rzecz jasna ma to kiepski wpływ na zużycie pamięci, a także (nieco mniejszy) na prędkość. Inne rozwiązanie, to użyć set i udawać, że to kopiec. Zamiast top(), można używać .front(), zamiast .push(), można używać insert(), konstruktory są podobne, a zamiast .pop(), można użyć s.erase(s.begin()). Trzeba jednak pamiętać, że będzie to działało wolniej niż kopiec, choć w teorii złożoność wszystkich operacji jest identyczna. Nawet budowanie "kopca", poprzez podanie zakresu powinno działać w O(1). To co zyskujemy, to możliwość usunięcia w dowolnym momencie dowolnego elementu. Kolejny problem, to niemożność scalenia ze sobą dwóch kolejek w jedną. Algorytmy wymagające złączanych kolejek to rzadkość, nie mniej gdyby się takowy przytrafiło Wam implementować, to zapewne trzeba będzie napisać własne Drzewa Lewicowe, albo próbować zlepiać drzewka czerwono-czarne. |
||||||||||||||||
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com