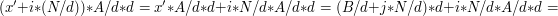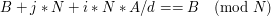gcd
20.11.2009
 Omówiliśmy sobie Algorytm Euklidesa i parę jego zastosowań. Polecam gorąco artykuł Damiana Rusaka. Kto się nie spóźnił, załapał się na wersję nie używającą dzielenia, znacznie prostszą w analizie złożoności czasowej:
Przypomnieliśmy sobie też wersję z modulo i prosiłem, aby każdy w domu pomyślał nad podobnym dowodem dla tejże wersji. Przypominam, że powinno wyjść Zaczęliśmy jednak od zagadki: jaka jest ostatnia cyfra ilorazu liczb naturalnych, kończących się odpowiednio na 6 i 2. Pokazaliśmy jak rozwiązać tę zagadkę gdy dzielimy przez liczbę względnie pierwszą z 10 i zobaczyliśmy, że przydaje się do tego Okrojony Rozszerzony Algorytm Euklidesa.
Obiecałem wyjaśnić, skąd wiemy, że dla 6 i 2, poprawnymi wynikami są akurat 3 i 8. Szerzej interesuje nas następujący problem. Dla zadanych A,B i N chcemy znaleźć wszystkie takie x, że
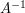 , a następnie mnożymy obustronnie nasze równanie i otrzymujemy: , a następnie mnożymy obustronnie nasze równanie i otrzymujemy:
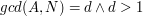 . .
Sytuacja wygląda wtedy tak:
Sytuacja nie jest jednak beznadziejna, gdyż to co możemy zrobić, to podzielić przez d również N. Otrzymamy wtedy:
Rozwiązując to nowe równanie poznamy resztę z dzielenia x przez (N/d). To nie jest to czego szukaliśmy, bo chcieliśmy poznać resztę z dzielenia przez N. Istnieje aż d różnych reszt z dzielenia przez N, które spełniają ten warunek. Okazuje się, że każda z nich jest dobra. Wracając do naszego przykładu. Rozwiążemy :
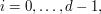 aby uzyskać wszystkie poprawne reszty modulo N.
Ale dlaczego tak jest, że każda z nich jest dobra? aby uzyskać wszystkie poprawne reszty modulo N.
Ale dlaczego tak jest, że każda z nich jest dobra?
Jest tak, bo są one postaci
|
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


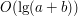 .
Pokazaliśmy sobie też przypadek wymagający
.
Pokazaliśmy sobie też przypadek wymagający 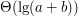 .
.
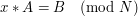
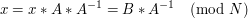
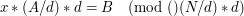
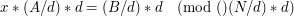
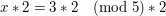
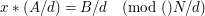
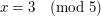
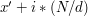 , gdzie
, gdzie 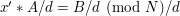 , co po podstawieniu do oryginalnego równania daje:
, co po podstawieniu do oryginalnego równania daje: