Graf, to pojęcie, które jest fundamentalne dla zrozumienia większości olimpijskich problemów i ich rozwiązań. Definicję na pewno znajdziecie w sieci, a większość opracowań zadań używa go bez zbędnych wyjaśnień.
Formalnie, graf jest parą. Piszemy 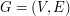 mając na myśli, że graf
mając na myśli, że graf 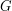 jest parą, której pierwszym elementem jest
jest parą, której pierwszym elementem jest 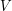 a drugim
a drugim 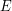 . Graf jest parą, której pierwszym elementem jest zbiór wierzchołków, a drugim pewna relacja. Relacja to pojęcie fundamentalne dla logiki i wiele ciekawych matematycznych pojęć jak "porządek", czy "klasa abstrakcji", bazują na nim. Formalnie relacja k-argumentowa to pewien podzbiór zawarty w iloczynie kartezjańskim k zbiorów. Taka formalna definicja pewnie nieco odstrasza, a nam nie jest potrzebna w całym brzmieniu, bo interesować nas będą tylko relacje 2-argumentowe, czyli binarne, czyli "strzałki" prowadzące od jednego argumentu do drugiego. Zbiór krawędzi jest relacją dwuargumentową która zachodzi pomiędzy elementami
. Graf jest parą, której pierwszym elementem jest zbiór wierzchołków, a drugim pewna relacja. Relacja to pojęcie fundamentalne dla logiki i wiele ciekawych matematycznych pojęć jak "porządek", czy "klasa abstrakcji", bazują na nim. Formalnie relacja k-argumentowa to pewien podzbiór zawarty w iloczynie kartezjańskim k zbiorów. Taka formalna definicja pewnie nieco odstrasza, a nam nie jest potrzebna w całym brzmieniu, bo interesować nas będą tylko relacje 2-argumentowe, czyli binarne, czyli "strzałki" prowadzące od jednego argumentu do drugiego. Zbiór krawędzi jest relacją dwuargumentową która zachodzi pomiędzy elementami 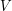 .
.
Formalnie powiedzielibyśmy, że zbiór 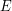 zawiera się w
zawiera się w 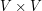 , czyli w iloczynie kartezjańskim zbioru
, czyli w iloczynie kartezjańskim zbioru 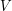 z nim samym. Krzyżyk oznacza iloczyn kartezjański. Definicję oczywiście znaleźć można w sieci, ale nam wystarczy do szczęścia rozumieć to poprzez następującą analogię do języka C++: jeśli mamy jakieś dwa typy S oraz T, to
z nim samym. Krzyżyk oznacza iloczyn kartezjański. Definicję oczywiście znaleźć można w sieci, ale nam wystarczy do szczęścia rozumieć to poprzez następującą analogię do języka C++: jeśli mamy jakieś dwa typy S oraz T, to
reprezentuje iloczyn kartezjański zbioru T i zbioru S, bowiem do zbioru elementów o typie pair<T,S> należą takie pary p, że p.first ma typ

, zaś p.second ma typ
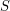
.
Mniej formalnie mówimy, że
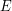
to taki zbiór strzałek pomiędzy elementami V.
Zbiór wierzchołków, może być dowolnym zbiorem, ale najczęściej interesują nas skończone zbiory. Elementy skończonego zbioru najwygodniej jest sobie ponumerować liczbami naturalnymi od 1 do n, gdzie 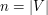 jest liczbą elementów zbioru V. Nawet jeśli w zadaniu pojawia się graf, którego elementy mają inne nazwy (np. miasta, których nazwy to jakieś słowa) to i tak lepiej jest myśleć o liczbach.
jest liczbą elementów zbioru V. Nawet jeśli w zadaniu pojawia się graf, którego elementy mają inne nazwy (np. miasta, których nazwy to jakieś słowa) to i tak lepiej jest myśleć o liczbach.
Podobnie krawędzie, choć często w zadaniu nazywają się "drogami", "korytarzami", "znajomościami", czy jeszcze inaczej, najprościej nazywać krawędziami i myśleć o nich jak o parach liczb.
Grafy dzielimy na skierowane i nieskierowane. Graf nieskierowany to taki, w którym każda krawędź 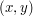 posiada swoją bliźniaczą krawędź
posiada swoją bliźniaczą krawędź 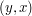 . Formalnie mówimy, wtedy że relacja E jest symetryczna. Grafy nieskierowane często rysujemy przy pomocy kresek a nie strzałek, rozumiejąc, że taka kreska oznacza krawędź w obie strony. W zadaniach często pojawiają się "drogi jednokierunkowe" bądź "korytarze dwukierunkowe" i wtedy od razu wiemy, czy mowa jest o grafie skierowanym czy nieskierowanym.
. Formalnie mówimy, wtedy że relacja E jest symetryczna. Grafy nieskierowane często rysujemy przy pomocy kresek a nie strzałek, rozumiejąc, że taka kreska oznacza krawędź w obie strony. W zadaniach często pojawiają się "drogi jednokierunkowe" bądź "korytarze dwukierunkowe" i wtedy od razu wiemy, czy mowa jest o grafie skierowanym czy nieskierowanym.
Przykłady:
Graf skierowany, który wygląda jak trójkąt, możemy nazwać T i napisać 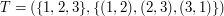 , a więc
, a więc 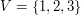 ,
, 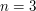 ,
, 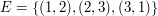 ,
, 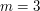 .
.
Jak widać, zbiory oznaczamy nawiasami wąsatymi: 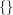 , zaś pary nawiasami okrągłymi
, zaś pary nawiasami okrągłymi 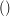 . Różnica między parą a zbiorem dwuelementowym jest taka, że w zbiorze kolejność elementów nie ma znaczenia a więc
. Różnica między parą a zbiorem dwuelementowym jest taka, że w zbiorze kolejność elementów nie ma znaczenia a więc 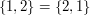 , podczas gdy w parach ma znaczenie:
, podczas gdy w parach ma znaczenie: 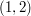 to nie to samo co
to nie to samo co 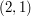 . Dlatego też o krawędziach nieskierowanych myśli się niekiedy jak o zbiorach dwuelementowych, podczas gdy o krawędziach skierowanych jak o parach.
. Dlatego też o krawędziach nieskierowanych myśli się niekiedy jak o zbiorach dwuelementowych, podczas gdy o krawędziach skierowanych jak o parach.
Graf nieskierowany, który wygląda jak kwadrat, możemy nazwać K i napisać 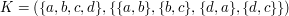 .
.

 , zaś p.second ma typ
, zaś p.second ma typ 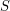 .
.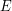 to taki zbiór strzałek pomiędzy elementami V.
to taki zbiór strzałek pomiędzy elementami V.


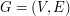 mając na myśli, że graf
mając na myśli, że graf 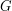 jest parą, której pierwszym elementem jest
jest parą, której pierwszym elementem jest 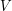 a drugim
a drugim 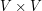 , czyli w iloczynie kartezjańskim zbioru
, czyli w iloczynie kartezjańskim zbioru 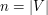 jest liczbą elementów zbioru V. Nawet jeśli w zadaniu pojawia się graf, którego elementy mają inne nazwy (np. miasta, których nazwy to jakieś słowa) to i tak lepiej jest myśleć o liczbach.
jest liczbą elementów zbioru V. Nawet jeśli w zadaniu pojawia się graf, którego elementy mają inne nazwy (np. miasta, których nazwy to jakieś słowa) to i tak lepiej jest myśleć o liczbach.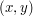 posiada swoją bliźniaczą krawędź
posiada swoją bliźniaczą krawędź 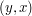 . Formalnie mówimy, wtedy że relacja E jest symetryczna. Grafy nieskierowane często rysujemy przy pomocy kresek a nie strzałek, rozumiejąc, że taka kreska oznacza krawędź w obie strony. W zadaniach często pojawiają się "drogi jednokierunkowe" bądź "korytarze dwukierunkowe" i wtedy od razu wiemy, czy mowa jest o grafie skierowanym czy nieskierowanym.
. Formalnie mówimy, wtedy że relacja E jest symetryczna. Grafy nieskierowane często rysujemy przy pomocy kresek a nie strzałek, rozumiejąc, że taka kreska oznacza krawędź w obie strony. W zadaniach często pojawiają się "drogi jednokierunkowe" bądź "korytarze dwukierunkowe" i wtedy od razu wiemy, czy mowa jest o grafie skierowanym czy nieskierowanym.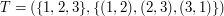 , a więc
, a więc 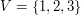 ,
, 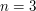 ,
, 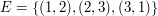 ,
, 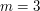 .
.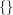 , zaś pary nawiasami okrągłymi
, zaś pary nawiasami okrągłymi 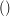 . Różnica między parą a zbiorem dwuelementowym jest taka, że w zbiorze kolejność elementów nie ma znaczenia a więc
. Różnica między parą a zbiorem dwuelementowym jest taka, że w zbiorze kolejność elementów nie ma znaczenia a więc 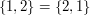 , podczas gdy w parach ma znaczenie:
, podczas gdy w parach ma znaczenie: 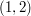 to nie to samo co
to nie to samo co 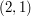 . Dlatego też o krawędziach nieskierowanych myśli się niekiedy jak o zbiorach dwuelementowych, podczas gdy o krawędziach skierowanych jak o parach.
. Dlatego też o krawędziach nieskierowanych myśli się niekiedy jak o zbiorach dwuelementowych, podczas gdy o krawędziach skierowanych jak o parach.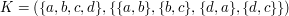 .
.

