Liczby pierwsze
27.11.2009
 Analizując złożoność sita Erastotenesa, natrafiliśmy na dość częstego bohatera: liczby harmoniczne:
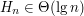 , co da się pokazać prosto dla n będących potęgami dwójki, a następnie dla pozostałych korzystając z tego że , co da się pokazać prosto dla n będących potęgami dwójki, a następnie dla pozostałych korzystając z tego że 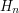 jest monotoniczną funkcją jest monotoniczną funkcją  : :
oraz
Powiedzieliśmy sobie o kilku możliwych optymalizacjach:
Próbowałem też wyjaśnić jak pomysł z przeskakiwaniem liczb parzystych rozszerzyć, na kolejne liczby pierwsze. Na początek pogadaliśmy trochę o Chińskim Twierdzeniu o Resztach, które (w dość niekonstruktywny sposób) mówi tyle, że jeśli mamy kilka liczb (względnie) pierwszych, to każda kombinacja reszt z dzielenia przez nie zdarza się dokładnie jeden raz wśród liczb naturalnych mniejszych od ich iloczynu. Po prawdzie, zdarza się dokładnie raz w każdym przedziale o tej długości. Ciekawym zadaniem jest wcielenie się w generała który ryzykując głową przed Cesarzem musi mu zdać raport na temat liczby żołnierzy. O tym jak na podstawie reszt skonstruować liczbę, która ma takie reszty, na razie sobie nie mówiliśmy, ale podpowiem, że przydatne jest do tego liczenie odwrotności.
Jednym z wniosków z tego twierdzenia jest fakt, że jeśli skreślimy liczby parzyste, podzielne przez 3 oraz podzielne przez 5, to pozostanie nam 1/2* 2/3 * 4/5 wszystkich liczb.
Ogólnie jeśli użyjemy liczb pierwszych Prowadzi to mniej więcej do takiego algorytmu znajdującego wszystkie liczby pierwsze mniejsze od n.
Tutaj może jeszcze taka uwaga, że to skreślanie wielokrotności
Co nam to wszystko daje? W sumie to nie wiem, bo nie próbowałem i zachęcam do eksperymentów. Eksperymentujac warto porównywać wyniki z programem wzorcowym.
Teoretycznie można liczyć, że w każdej pętli wykonamy tylko
Tak czy owak powinno nam zależeć, aby stosunek |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


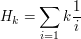
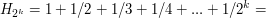
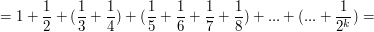
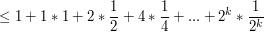
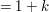
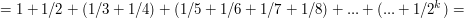
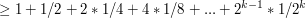
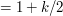
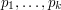 , to pozostanie nam
, to pozostanie nam 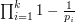 wszystkich liczb spośród tych mniejszych od
wszystkich liczb spośród tych mniejszych od 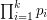 . Po prawdzie działa to dla każdego przedziału o tej długości.
. Po prawdzie działa to dla każdego przedziału o tej długości.
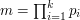
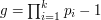
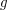 liczb z zakresu
liczb z zakresu 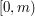 , które nie dzielą się przez żadną z liczb
, które nie dzielą się przez żadną z liczb 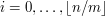
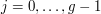
![$ p=i*m+T[j] $](/files/tex/f9d77698fe02dae9e56f975e417b845da19ac784.png) jest mniejsze od n i nie jest skreślone, to wypisz
jest mniejsze od n i nie jest skreślone, to wypisz  i skreśl jego wielokrotności
i skreśl jego wielokrotności![$ (1+i*m+T[j])*p $](/files/tex/5aa2096e4189f3bec02ccb8db1152bfe4f4209db.png)
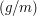 iteracji w porównaniu do oryginalnego algorytmu.
Zarówno w tej zewnętrznej (szukającej liczb pierwszych) jak i tej wewnętrznej (skreślającej jej wielokrotności).
Wydawać by się zatem mogło, że łączne przyspieszenie to
iteracji w porównaniu do oryginalnego algorytmu.
Zarówno w tej zewnętrznej (szukającej liczb pierwszych) jak i tej wewnętrznej (skreślającej jej wielokrotności).
Wydawać by się zatem mogło, że łączne przyspieszenie to 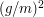 , ale oczywiście tak nie jest (dlaczego?).
, ale oczywiście tak nie jest (dlaczego?).
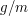 był jak najmniejszy.
Wynosi on
był jak najmniejszy.
Wynosi on 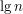 .
.


