Algorytmy grafowe, tekstowe i granica
04.12.2009
 Poznaliśmy pojęcie automatu skończonego, czyli czegoś co składa się z:
Automat można sobie wyobrażać jako grę planszową, na której jest jeden pionek, zaś zamiast rzutów kostką, mamy wczytywane kolejno literki mówiące nam jaki ruch na planszy należy wykonać. Wygrywamy, cieszymy się, jeśli akurat jesteśmy w polu oznaczonym jako akceptujące. Jeśli brak strzałki etykietowanej wczytaną literką, to "wybuchamy" i nie akceptujemy już nigdy niczego, co odpowiada koncepcji "idziesz do więzienia, nie przechodzisz przez start i nie dostajesz premii" tudzież tkwienia w tym więzieniu do końca świata. Zbiory słów nazwaliśmy językami, początek słowa prefiksem, a koniec sufiksem. Powiedzieliśmy sobie, choć bez dowodu, że język akceptowany przez automat skończony da się (i wygodnie jest) opisywać wyrażeniami regularnymi. Również bez dowodu, powiedzieliśmy sobie, że jeśli coś da się opisać wyrażeniem regularnym, to da się zbudować automat skończony, który to rozpoznaje. Na nasze skromne potrzeby wystarczy nam jednak delikatniejsze twierdzenie: dla dowolnego wzorca, język słów, których prefiksem jest dany wzorzec, da się rozpoznawać automatem skończonym.
Na razie na kilku przykładach zobaczyliśmy to w praktyce. Okazuje się, że jeśli wzorzec ma
Powiedzieliśmy sobie, że funkcję przejścia Po zajęciach pojawiło się zupełnie niespodziewane pytanie o to czy mógłbym pokazać przykład ciągu, który spełnia
Myślę, że może choć to zaskakujące, ów problem ma trochę związku z grafami i trochę z tekstami. Po pierwsze, przestrzenie metryczne można sobie wyobrażać jako grafy (być może nieskończone, jeśli taka jest przestrzeń). Wierzchołki odpowiadają elementom przestrzeni, zaś każda para wierzchołków jest połączona nieskierowaną krawędzią etykietowaną jej długością czyli odległością między elementami w przestrzeni. Przestrzeń metryczna musi spełniać pewne warunki, z których najważniejszy to nierówność trójkąta, czyli, żeby najkrótszą ścieżką między dwoma wierzchołkami grafu była po prostu łącząca je krawędź.
Intuicja podpowiada mi więc, że chciałbym zbudować taki (nieskończony) graf, w którym odległość między
Łatwo przekonać się, że o ile zdefiniujemy odległość od samego siebie jako 0, to powyższa funkcja definiuje metrykę, bo spełnia nierówność trójkąta.
Jednocześnie widać, że ciąg
Można sobie zadać pytanie: super, ale czy taka przestrzeń w ogóle ma jakieś realne zastosowania? Czy da się ją pokazać na jakimś naturalnym przykładzie?
Otóż, weźmy sobie zbiór wszystkich napisów (stringów).
Jak wiadomo napisy można porównywać. Jeśli się nie różnią, to powiemy, że odległość między nimi to 0. Jeśli różnią się na Tak na prawdę sztuczka polega po prostu na tym, że granica nie należy do przestrzeni. Można więc znaleźć prostszy przykład. Weźmy po prostu wszystkie liczby rzeczywiste oprócz g. Weźmy teraz dowolny ciąg, który zbiega do g, ale nie zawiera g na żadnej pozycji. Wtedy taki ciąg jest zbieżny w pierwszym sensie, ale nie w drugim, bo granica nie należy do przestrzeni. Jednocześnie sam fakt wyrzucenia g z przestrzeni, wcale nie psuje tego, że |x-y| to całkiem poprawna metryka. |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


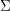 , czyli alfabetu, czyli skończonego zbioru znaczków jakie mogą się pojawić na drodze robaczka
, czyli alfabetu, czyli skończonego zbioru znaczków jakie mogą się pojawić na drodze robaczka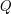 , czyli stanów, czyli skończonego zbioru pewnych abstrakcyjnych konfiguracji pamięci robaczka
, czyli stanów, czyli skończonego zbioru pewnych abstrakcyjnych konfiguracji pamięci robaczka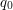 , czyli stanu początkowego,
, czyli stanu początkowego, 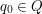 z jakim rodzi się robaczek
z jakim rodzi się robaczek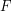 , czyli stanów akceptujących,
, czyli stanów akceptujących, 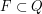
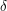 , czyli funkcji przejścia,
, czyli funkcji przejścia, 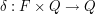 , opisującej proces kognitywny robaczka, czyli w jaki sposób życie wpływa na jego wiedzę
, opisującej proces kognitywny robaczka, czyli w jaki sposób życie wpływa na jego wiedzę liter, to wystarczy nam
liter, to wystarczy nam 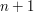 stanów. Stan
stanów. Stan 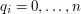 interpretujemy w następujący sposób. Najdłuższy sufiks przeczytanego dotąd prefiksu będący prefiksem szukanego wzorca ma długość
interpretujemy w następujący sposób. Najdłuższy sufiks przeczytanego dotąd prefiksu będący prefiksem szukanego wzorca ma długość  .
.
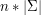 , czyli w praktyce pewnie 256 razy więcej niż byśmy chcieli.
Zadanie domowe polega na wymyśleniu jak w ogóle wyliczyć i stablicować funkcję
, czyli w praktyce pewnie 256 razy więcej niż byśmy chcieli.
Zadanie domowe polega na wymyśleniu jak w ogóle wyliczyć i stablicować funkcję 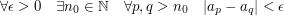
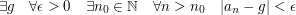
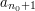 i
i 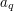 dla
dla 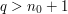 , zależy tylko od
, zależy tylko od 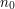 . Tzn chciałbym aby wszyscy byli w tej samej odległości od
. Tzn chciałbym aby wszyscy byli w tej samej odległości od 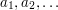 , zaś odległość jest zdefiniowana tak:
, zaś odległość jest zdefiniowana tak:
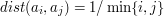
 bez trudu wskażemy takie
bez trudu wskażemy takie 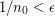 .
Widać też, że nie jest spełniony drugi warunek, czyli nie istnieje granica tego ciągu.
.
Widać też, że nie jest spełniony drugi warunek, czyli nie istnieje granica tego ciągu.
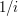 .
Łatwo przekonać się, że tak zdefiniowana przestrzeń i odległość spełniają warunek trójkąta i mamy tu do czynienia z metryką.
Jednocześnie widać, że ciąg napisów: "a", "aa", "aaa", "aaaa",
.
Łatwo przekonać się, że tak zdefiniowana przestrzeń i odległość spełniają warunek trójkąta i mamy tu do czynienia z metryką.
Jednocześnie widać, że ciąg napisów: "a", "aa", "aaa", "aaaa", 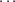 nie ma granicy. Granicą chciałby być napis złożony z nieskończenie wielu literek 'a', ale to niestety nie jest poprawny napis.
nie ma granicy. Granicą chciałby być napis złożony z nieskończenie wielu literek 'a', ale to niestety nie jest poprawny napis.


