UnionFind
13.11.2009
 Na zajęciach poznaliśmy też inną struktruę danych, która posiada "explicit layout", jaką jest union-find, zaimplementowany jako pojedyncza tablica.
Tu dygresja jest taka, że memset jako drugi argument bierze pojedynczy bajt, więc to, że ten kod działa wynika tylko z tego, że czterobajtowy zapis liczby -1, wygląda tak samo jak 4 zapisy jednobajtowej liczby -1 pod rząd. Jako ćwiczenie można sobie zaimplementować funkcję find.
Oto jedno z moich ulubionych zadanek pochodzące z 10 Olimpiady Informatycznej Małpki. Zadanko jest dostępne na MAINie SIO. Powiedzieliśmy sobie też, z grubsza co to jest logartym iterowany, oraz, że analiza złożoności dla problemu Union-Find do najłatwiejszych nie należy. Kluczowe jednak są pewne prawdy objawione:
Prawda jest taka, że Union-Find działa bardzo szybko i że nie chodzi nawet o logarytm iterowany, tylko o odwrotność funkcji Ackermana. Prawda jest też taka, że żeby móc coś sensownie mówić o złożoności, to wypada powiedzieć ile operacji union, a ile operacji find, chcemy zrobić. Nie mniej, do naszych ziemskich celów, wystarczy wiedzieć, że to jest po prostu mniej niż 4.
|
||||||||||
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


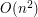 , chociaż program nadal będzie działał
, chociaż program nadal będzie działał

