Mosty i punkty artykulacji
02.10.2010 - Michał Karpiński
  Umiejętność wyszukiwania mostów i punktów artykulacji przydaje się nie tylko w konkursach algorytmicznych. Wszędzie tam, gdzie mamy do czynienia ze strukturą grafu np. sieć dróg, torów kolejowych, kabli internetowych wiedza zawarta w niniejszym artykule okazuje się niezbędna. Można śmiało powiedzieć, że temat, którym się będziemy zajmować to kolejny ważny krok na drodze do zostania mistrzem teorii grafów. Definicje mostu i punktu artykulacji są bardzo podobne. Najpierw zabierzemy się za most. Jednak zanim podane zostaną jakiekolwiek matematyczne pojęcia, naszą zabawę rozpoczniemy od krótkiej historyjki. W pewnym małym miasteczku o nazwie Bajtowo zamontowano sieć telefoniczną, dzięki której mieszkańcy mogli się między sobą porozumieć. Sieć ta działa w bardzo nietypowy sposób. Zamiast wybudować centralną jednostkę, do której podłączony byłby każdy telefon z osobna, mieszkańcy wpadli na pomysł aby połączyć ze sobą telefony w sposób losowy: 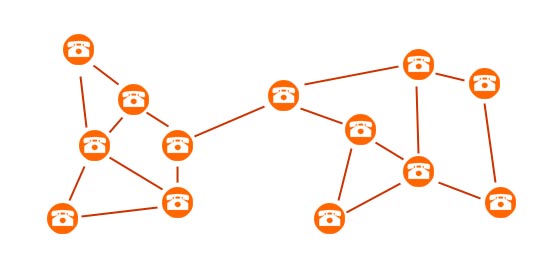 Przy takim połączeniu każdy w miasteczku może dodzwonić się do wszystkich sąsiadów. Wszystko byłoby dobrze, gdyby nie fakt, że w Bajtowie często występują burze i silne wiatry, które łatwo mogą pozrywać kable telefoniczne. Problem pojawia się gdy zerwany zostanie taki kabel, który uniemożliwi niektórym mieszkańcom na wykonanie połączeń do jakiejś oddzielonej części Bajtowa. Mieszkańcy wpadli na pomysł, żeby do niektórych kabli zastosować dodatkową izolację, która mogłaby oprzeć się siłą natury. Taka izolacja niestety kosztuje. Zadanie polega na tym, aby założyć izolację tylko na jeden istotny kabel, czyli taki, po którego zerwaniu sieć telefoniczna staje się niespójna. Po krótkiej analizie powyższego rysunku nietrudno wskazać taki kabel: 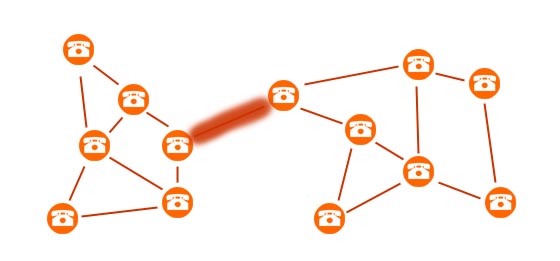 Łatwo jest zauważyć, że jeśli dowolny inny kabel zostałby zniszczony, to cała sieć nie ucierpiałaby na tym. Jak pewnie każdy już się domyśla - w grafie zbudowanym z powyższej sieci telefonicznej - kabel, który wybraliśmy jest mostem. Dla formalności podamy jeszcze definicję: Most – jest to krawędź w grafie nieskierowanym, po której usunięciu graf się rozspójnia. Innymi słowy: jest to taka krawędź, że jeśli wyciągniemy ją z grafu, to zwiększy się liczba spójnych składowych.
(11 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com