Mosty i punkty artykulacji
02.10.2010 - Michał Karpiński
  Zadanie ze sprawdzaczkąPoniżej znajdują się proste zadania do napisania na komputerze, które związane są z wyszukiwaniem mostów i punktów artykulacji. Zachęcam do sprawdzenia nabytej wiedzy w praktyce. Zadanie 1 - "Grafy mostowo-silne"Mamy dany graf nieskierowany. Przyjmijmy następujące definicje: most jest silny, jeśli na obu jego końcach znajdują się punkty artykulacji. Z drugiej strony most nazywamy słabym, jeśli tylko jeden (lub żaden) z jego końców jest punktem artykulacji. Graf mostowo-silny to taki, który zawiera więcej mostów silnych niż słabych. Zadaniem jest stwierdzić, czy podany graf jest mostowo-silny. WejścieW pierwszym wierszu podane są dwie liczby WyjścieOdpowiedzią ma być jedna linia z napisem TAK, jeśli graf jest mostowo-silny lub NIE w przeciwnym wypadku. Przykład 1Wejście: Wyjście: Przykład 2Wejście: Wyjście: Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany. Zaloguj się lub załóż konto.
Zadanie 2 - "K-długie-mosty"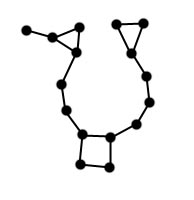
K-długim-mostem nazywamy drogę prostą w grafie nieskierowanym, która złożona jest jedynie z WejścieW pierwszym wierszu podane są dwie liczby WyjścieDla Przykład 1Wejście: Wyjście: Przykład 2Wejście: Wyjście: Przykład 3Wejście: Wyjście: Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany. Zaloguj się lub załóż konto.
(11 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


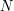 i
i 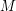 oddzielone spacją (gdzie
oddzielone spacją (gdzie 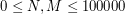 ).
).  co oznacza, że istnieje krawędź z wierzchołka
co oznacza, że istnieje krawędź z wierzchołka  do wierzchołka
do wierzchołka  (pamiętamy, że graf wejściowy jest nieskierowany).
(pamiętamy, że graf wejściowy jest nieskierowany).  mostów. Zawsze rozpatrujemy najdłuższą taką drogę. Dla przykładu: na grafie obok znajduje się 1-długi-most, 3-długi-most i 4-długi-most. Zadaniem jest wyznaczenie wszystkich k-długich-mostów (dla dowolnego
mostów. Zawsze rozpatrujemy najdłuższą taką drogę. Dla przykładu: na grafie obok znajduje się 1-długi-most, 3-długi-most i 4-długi-most. Zadaniem jest wyznaczenie wszystkich k-długich-mostów (dla dowolnego  różnych k-długich-mostów należy wypisać
różnych k-długich-mostów należy wypisać 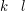 co oznacza, że w grafie znajduje się dokładnie
co oznacza, że w grafie znajduje się dokładnie 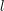 różnych k-długich-mostów. Wiersze mają być wypisane rosnąco w zależności od
różnych k-długich-mostów. Wiersze mają być wypisane rosnąco w zależności od 

