W poszukiwaniu mostów cd.
Zbierając do kupy wszystkie nasze rozważania z poprzedniej strony można wywnioskować, że poniższe zdanie jest prawdziwe:
Krawędź z grafu 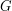 jest mostem wtedy i tylko wtedy, gdy nie leży na żadnym cyklu prostym w grafie
jest mostem wtedy i tylko wtedy, gdy nie leży na żadnym cyklu prostym w grafie 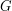 .
.
Więcej informacji na temat przeszukiwania w głąb znajdziesz w tym artykule
To twierdzenie w znaczący sposób ułatwi nam konstruowanie algorytmu, ponieważ problem znajdowania mostów sprowadza się do problemu znajdowania cykli w grafie nieskierowanym. W takim razie wejściowy graf należy przeszukiwać w głąb.
Przeszukujemy graf metodą DFS. Na pewno każdy się zgodzi, że jeśli w grafie istnieją jakiekolwiek mosty, to należą one do lasu przeszukiwania w głąb. Jest tak dlatego, że wszystkie krawędzie nie należące do żadnego drzewa przeszukiwania w głąb są krawędziami wtórnymi: czyli po dodaniu ich do któregoś z drzew utworzyłyby cykl, a przecież z powyższego twierdzenia wiemy, że żaden most nie leży na cyklu.
Mówiąc wprost: rozpatrujemy tylko krawędzie, przez które przechodziliśmy podczas przeszukiwania grafu metodą DFS.
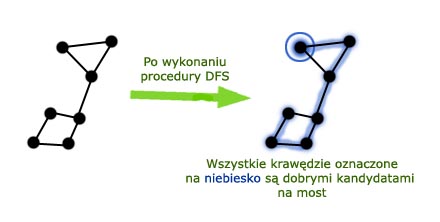
Funkcja „Low”
Większość krawędzi należących do lasu przeszukiwania w głąb raczej nie ma szans być mostami (przykładem jest powyższy rysunek, gdzie tylko jedna krawędź jest mostem). Żeby wyodrębnić poszukiwane przez nas krawędzie wprowadzimy dodatkowy atrybut dla każdego wierzchołka. Atrybut ten nazwiemy 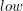 (czyt. loł), czyli "niski".
(czyt. loł), czyli "niski".
Poniższy fragment może wydawać się z początku trudny - nie zniechęcaj się jednak - po paru akapitach wszystko stanie się jaśniejsze.
![$ low[v] $](/files/tex/2e538d60bddeb39962b9af8d82177af4d9c92a6c.png) obliczamy zaczynając od liści drzewa przeszukiwania w głąb (idąc aż do korzenia) w następujący sposób:
obliczamy zaczynając od liści drzewa przeszukiwania w głąb (idąc aż do korzenia) w następujący sposób:
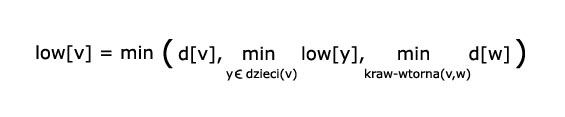
Przypominamy, że ![$ d[v] $](/files/tex/115edd3c5063780310d2d9d18ef003a1d361c801.png) jest to czas odwiedzenia wierzchołka
jest to czas odwiedzenia wierzchołka  podczas przeszukiwania grafu w głąb
podczas przeszukiwania grafu w głąb
Na pierwszy rzut oka podany wzór wydaje się być skomplikowany. Powstaje pytanie: po co w ogóle stosujemy tego typu udziwnienia? Okazuje się, że wcale nie komplikujemy sobie zadania, a po wyliczeniu ![$ low[v] $](/files/tex/2e538d60bddeb39962b9af8d82177af4d9c92a6c.png) dla każdego
dla każdego  w łatwy sposób będziemy mogli stwierdzić, które krawędzie są mostami.
w łatwy sposób będziemy mogli stwierdzić, które krawędzie są mostami.
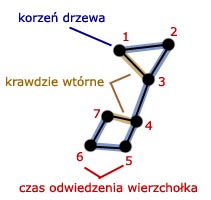
Zamiast tłumaczyć słownie (co byłoby nudne i niezrozumiałe), pozwolę sobie przedstawić działanie i znaczenie atrybutu 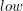 na prostym przykładzie. Weźmy graf z rysunku powyżej. Oznaczmy w nim drzewo przeszukiwania w głąb, krawędzie wtórne oraz atrybut
na prostym przykładzie. Weźmy graf z rysunku powyżej. Oznaczmy w nim drzewo przeszukiwania w głąb, krawędzie wtórne oraz atrybut 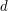 (czas odwiedzenia) dla każdego wierzchołka (patrz rysunek obok). Obliczamy atrybut
(czas odwiedzenia) dla każdego wierzchołka (patrz rysunek obok). Obliczamy atrybut  :
:
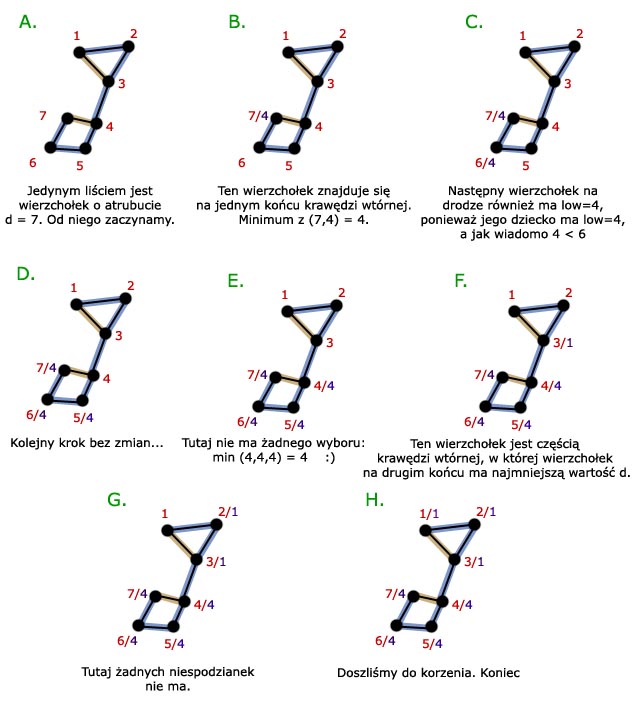
Atrybut  został wyliczony dla wszystkich wierzchołków. Nie łatwo jest wpaść na to, po co właściwie robiliśmy wszystkie te obliczenia, dlatego od razu podam wzór na wyciągniecie z grafu wszystkich mostów:
został wyliczony dla wszystkich wierzchołków. Nie łatwo jest wpaść na to, po co właściwie robiliśmy wszystkie te obliczenia, dlatego od razu podam wzór na wyciągniecie z grafu wszystkich mostów:
Dla każdego  należącego do
należącego do 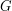 : jeśli
: jeśli ![$ d[v] = low[v] $](/files/tex/f163114be3a037bb7d6d8d140e4d11dffec158de.png) , to krawędź
, to krawędź ![$ \{p[v],v\} $](/files/tex/dcfb0454181212734b21fc38b31ed9e213c60274.png) jest mostem. (gdzie
jest mostem. (gdzie ![$ p[v] $](/files/tex/a04369f1e956f0360697ca7896e73a0506de55b5.png) jest poprzednikiem wierzchołka
jest poprzednikiem wierzchołka  w drzewie przeszukiwania w głąb)
w drzewie przeszukiwania w głąb)
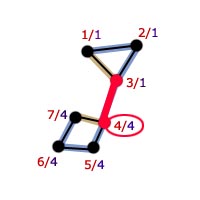
Spójrzmy na graf z naszego przykładu. Faktycznie jeden koniec mostu znajduje się w wierzchołku, który ma ![$ d[v] = low[v] $](/files/tex/f163114be3a037bb7d6d8d140e4d11dffec158de.png) . Zauważmy, że korzeń również spełnia tą zależność, ale nie posiada on poprzednika, dlatego nie może być częścią mostu.
. Zauważmy, że korzeń również spełnia tą zależność, ale nie posiada on poprzednika, dlatego nie może być częścią mostu.




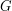 jest mostem wtedy i tylko wtedy, gdy nie leży na żadnym cyklu prostym w grafie
jest mostem wtedy i tylko wtedy, gdy nie leży na żadnym cyklu prostym w grafie 
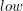 (czyt. loł), czyli "niski".
(czyt. loł), czyli "niski".![$ low[v] $](/files/tex/2e538d60bddeb39962b9af8d82177af4d9c92a6c.png) obliczamy zaczynając od liści drzewa przeszukiwania w głąb (idąc aż do korzenia) w następujący sposób:
obliczamy zaczynając od liści drzewa przeszukiwania w głąb (idąc aż do korzenia) w następujący sposób:
![$ d[v] $](/files/tex/115edd3c5063780310d2d9d18ef003a1d361c801.png) jest to czas odwiedzenia wierzchołka
jest to czas odwiedzenia wierzchołka  podczas przeszukiwania grafu w głąb
podczas przeszukiwania grafu w głąb
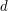 (czas odwiedzenia) dla każdego wierzchołka (patrz rysunek obok). Obliczamy atrybut
(czas odwiedzenia) dla każdego wierzchołka (patrz rysunek obok). Obliczamy atrybut 

![$ d[v] = low[v] $](/files/tex/f163114be3a037bb7d6d8d140e4d11dffec158de.png) , to krawędź
, to krawędź ![$ \{p[v],v\} $](/files/tex/dcfb0454181212734b21fc38b31ed9e213c60274.png) jest mostem. (gdzie
jest mostem. (gdzie ![$ p[v] $](/files/tex/a04369f1e956f0360697ca7896e73a0506de55b5.png) jest poprzednikiem wierzchołka
jest poprzednikiem wierzchołka 

