Mosty i punkty artykulacji
02.10.2010 - Michał Karpiński
  Dlaczego to działa?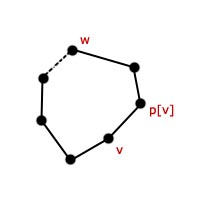
Znów przeprowadzimy dowód przez sprzeczność. Sprawdźmy co by się stało, gdyby dla pewnego wierzchołka Skorzystamy z faktu, że dla każdego wierzchołka Skoro W takim razie, gdy obliczamy funkcję Żeby oswoić się z nowo zdobytą wiedzą, prześledźmy jeszcze jeden przykład wyszukiwania mostów w postaci prostej animacji: 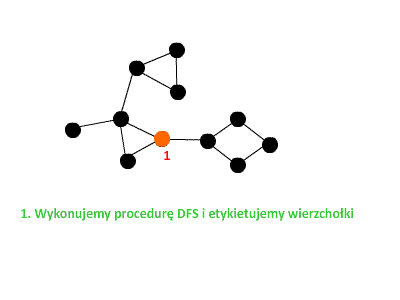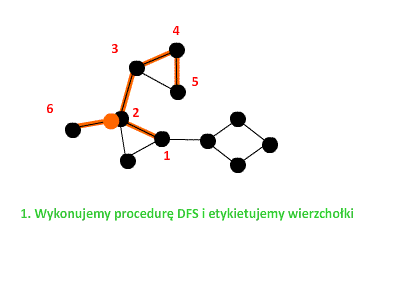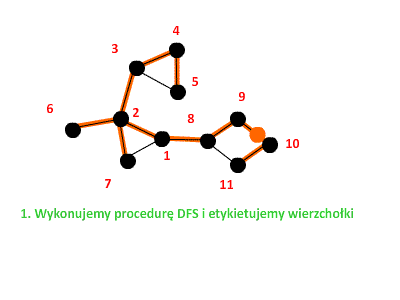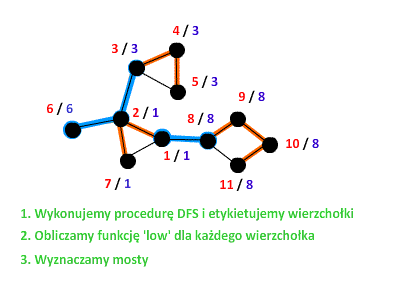 Na koniec przedstawimy wszystkie kroki algorytmu wyszukiwania mostów:
Do mostów wrócimy jeszcze pod koniec tego artykułu, gdzie będziemy wyznaczać złożoność czasową przedstawionych algorytmów. Punkty artykulacjiRozważania na temat punktów artykulacji rozpoczniemy bez większego wstępu. Przejdźmy od razu do definicji: Punktem artykulacji nazywamy taki wierzchołek, po którego usunięciu graf się rozspójni. Inaczej: po usunięciu tego wierzchołka zwiększy się liczba spójnych składowych w grafie wejściowym. Nie da się ukryć, że definicja punktu artykulacji jest niemal identyczna do definicji mostu. Jednak tym razem będziemy szukali wierzchołków, a nie krawędzi.  (11 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


 w grafie
w grafie 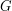 zachodziło
zachodziło ![$ d[v] = low[v] $](/files/tex/f163114be3a037bb7d6d8d140e4d11dffec158de.png) a krawędź
a krawędź ![$ e=\{p[v],v
\} $](/files/tex/072364df5bad9e66b3220b7cd4fcbc95b233b660.png) nie byłaby mostem.
nie byłaby mostem.![$ d[v] > d[p[v]] $](/files/tex/abe6cc1607d79fa9e49bff6371872af86528e599.png) . Ta relacja zachodzi w oczywisty sposób. Budując drzewo przeszukiwania w głąb przypisujemy etykiety czasowe o większej wartości wierzchołkom, które odwiedzamy później.
. Ta relacja zachodzi w oczywisty sposób. Budując drzewo przeszukiwania w głąb przypisujemy etykiety czasowe o większej wartości wierzchołkom, które odwiedzamy później. nie jest mostem, to należy do jakiegoś cyklu prostego. Innymi słowy: istnieje inna droga prowadząca do
nie jest mostem, to należy do jakiegoś cyklu prostego. Innymi słowy: istnieje inna droga prowadząca do ![$ p[v] $](/files/tex/a04369f1e956f0360697ca7896e73a0506de55b5.png) nie przechodząca przez
nie przechodząca przez 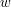 ).
).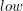 i dochodzimy do wierzchołka
i dochodzimy do wierzchołka ![$ low[v] \le d[p[v]] $](/files/tex/7719a1888556dc3ee412f4a476ad69e40b49da9d.png) – wynika to z powyższego faktu. Czyli
– wynika to z powyższego faktu. Czyli ![$ low[v] \neq d[v] $](/files/tex/69cd66db3c26e75758ebfde6b5859e38720ee1de.png) . Doszliśmy do sprzeczności.
. Doszliśmy do sprzeczności.![$ low[v] $](/files/tex/2e538d60bddeb39962b9af8d82177af4d9c92a6c.png) na podstawie wzoru z poprzedniej strony. Zaczynamy od liści drzewa przeszukiwania w głąb przechodząc w górę aż do korzenia
na podstawie wzoru z poprzedniej strony. Zaczynamy od liści drzewa przeszukiwania w głąb przechodząc w górę aż do korzenia![$ d[v]=low[v] $](/files/tex/235dc665927b5f8979a27600042c6a2aaaffceb1.png) wypisujemy, że krawędź
wypisujemy, że krawędź ![$ \{p[v],v\} $](/files/tex/dcfb0454181212734b21fc38b31ed9e213c60274.png) jest mostem (o ile
jest mostem (o ile 

