W poszukiwaniu punktów artykulacji
Podobieństwo między punktem artykulacji i mostem nie leży jedynie w definicji. Sposób znajdowania obu tych obiektów jest również bardzo podobny. Pierwsze dwa kroki algorytmu szukania punktów artykulacji jest taki sam jak przy wyznaczaniu mostów: wykonujemy procedurę DFS, a następnie wyliczamy funkcję 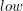 dla wszystkich wierzchołków. Inny natomiast jest krok trzeci, ale nie ma czym się martwić, gdyż jest on tak samo prosty jak przy szukaniu mostów.
dla wszystkich wierzchołków. Inny natomiast jest krok trzeci, ale nie ma czym się martwić, gdyż jest on tak samo prosty jak przy szukaniu mostów.
Zanim jednak podane zostanie rozwiązanie problemu wyszukiwania punktów artykulacji, przeprowadzimy dowody dwóch poniższych twierdzeń:
A. Korzeń drzewa przeszukiwania w głąb jest punktem artykulacji wtedy i tylko wtedy, gdy posiada on conajmniej dwóch synów.
B. Wierzchołek  nie będący korzeniem drzewa DFS jest punktem artykulacji wtedy i tylko wtedy, gdy przynajmniej dla jednego jego syna nie istnieje krawędź wtórna
nie będący korzeniem drzewa DFS jest punktem artykulacji wtedy i tylko wtedy, gdy przynajmniej dla jednego jego syna nie istnieje krawędź wtórna 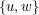 , taka że wierzchołek
, taka że wierzchołek  jest potomkiem
jest potomkiem  i
i 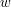 jest przodkiem
jest przodkiem  .
.
Zrozumienie dowodów tych twierdzeń nie jest wymagane, gdy zależy nam tylko na poznaniu gotowego algorytmu. Mimo wszystko gorąco zachęcam do przestudiowania następnych kilku akapitów.
Dowód twierdzenia A.
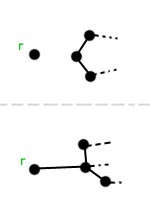
Najpierw udowodnimy implikację w prawo. Skorzystamy z prawa kontrapozycji i udowodnimy, że jeśli korzeń  drzewa DFS ma mniej niż dwóch synów, to nie może być punktem artykulacji. Jeśli
drzewa DFS ma mniej niż dwóch synów, to nie może być punktem artykulacji. Jeśli  jest korzeniem i nie ma dzieci, to nie posiada żadnych krawędzi z niego wychodzących. Po usunięciu wierzchołka
jest korzeniem i nie ma dzieci, to nie posiada żadnych krawędzi z niego wychodzących. Po usunięciu wierzchołka  nie zmieni się liczba spójnych składowych, więc
nie zmieni się liczba spójnych składowych, więc  nie jest punktem artykulacji. Gdy
nie jest punktem artykulacji. Gdy  posiada tylko jednego syna, to każdy inny wierzchołek w drzewie DFS jest osiągalny poprzez tego syna. Czyli usunięcie
posiada tylko jednego syna, to każdy inny wierzchołek w drzewie DFS jest osiągalny poprzez tego syna. Czyli usunięcie  nie zmieni liczby spójnych składowych, więc
nie zmieni liczby spójnych składowych, więc  nie jest punktem artykulacji.
nie jest punktem artykulacji.
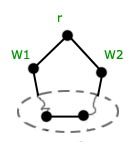
Implikację w lewą stronę udowodnimy przez sprzeczność. Załóżmy, że korzeń  ma dwóch synów
ma dwóch synów 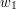 i
i 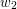 oraz
oraz  nie jest punktem artykulacji. Bez straty ogólności załóżmy, że
nie jest punktem artykulacji. Bez straty ogólności załóżmy, że 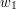 było odwiedzone wcześniej niż
było odwiedzone wcześniej niż 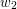 podczas działania procedury DFS. Skoro
podczas działania procedury DFS. Skoro  nie jest punktem artykulacji, to istnieje droga pomiędzy
nie jest punktem artykulacji, to istnieje droga pomiędzy 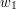 i
i 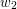 , która nie przechodzi przez
, która nie przechodzi przez  . Do wierzchołka
. Do wierzchołka 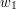 weszliśmy wcześniej, więc ta droga powinna zostać odwiedzona i
weszliśmy wcześniej, więc ta droga powinna zostać odwiedzona i 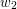 powinien być synem jakiegoś potomka
powinien być synem jakiegoś potomka 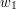 . Ale skoro
. Ale skoro 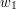 i
i 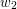 leżą na dwóch różnych poddrzewach korzenia
leżą na dwóch różnych poddrzewach korzenia  , to wiemy, że nie może istnieć inna droga pomiędzy tymi wierzchołkami. Dochodzimy do sprzeczności. Wierzchołek
, to wiemy, że nie może istnieć inna droga pomiędzy tymi wierzchołkami. Dochodzimy do sprzeczności. Wierzchołek  musi być zatem punktem artykulacji.
musi być zatem punktem artykulacji.
Dowód twierdzenia B.
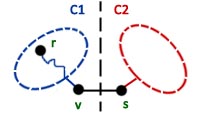
Dowód implikacji w prawo. Załóżmy, że  jest punktem artykulacji w grafie
jest punktem artykulacji w grafie 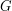 . Niech
. Niech 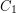 będzie spójną częścią grafu
będzie spójną częścią grafu 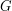 zawierającą korzeń
zawierającą korzeń  drzewa DFS. Niech
drzewa DFS. Niech  będzie sąsiadem
będzie sąsiadem  nie należącym do
nie należącym do 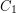 i niech
i niech 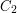 będzie spójną częścią grafu
będzie spójną częścią grafu 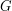 zawierającą
zawierającą  (taki sąsiad istnieje, bo usunięcie
(taki sąsiad istnieje, bo usunięcie  musi utworzyć przynajmniej dwie spójne składowe). W drzewie DFS wszyscy przodkowie
musi utworzyć przynajmniej dwie spójne składowe). W drzewie DFS wszyscy przodkowie  znajdują się w
znajdują się w 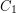 a wszyscy potomkowie
a wszyscy potomkowie  są w
są w 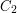 . Więc nie może istnieć żadna krawędź pomiędzy potomkami
. Więc nie może istnieć żadna krawędź pomiędzy potomkami  a przodkami
a przodkami  .
.
Dowód w lewo. Jeśli nie ma krawędzi wtórnej z wierzchołka  i żadnego jego potomka do któregokolwiek przodka
i żadnego jego potomka do któregokolwiek przodka  , to wiemy, że jedyna ścieżka z korzenia
, to wiemy, że jedyna ścieżka z korzenia  do
do  wiedzie przez
wiedzie przez  . Więc gdy usuniemy
. Więc gdy usuniemy  , graf rozspójni się. Czyli
, graf rozspójni się. Czyli  jest punktem artykulacji.
jest punktem artykulacji.
Algorytm wyszukiwania punktów artykulacji
Oto upragnione rozwiązanie:
- wykonujemy procedurę DFS
- wyliczamy funkcję
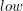 dla każdego wierzchołka (tak, jak podczas szukania mostów)
dla każdego wierzchołka (tak, jak podczas szukania mostów)
- wyznaczamy punkty artykulacji w dwóch krokach:
- sprawdzamy czy korzeń drzewa DFS posiada przynajmniej dwóch synów. Jeśli tak, to znaleźliśmy jeden z punktów artykulacji (Twierdzenie A).
- sprawdzamy wszystkie inne wierzchołki. Jeśli jakiś wierzchołek
 posiada syna
posiada syna  w drzewie DFS, takiego że
w drzewie DFS, takiego że ![$ low[s] \ge d[v] $](/files/tex/0cbd67a14f7c9d604a48782fee7237d0d78f0021.png) , wtedy
, wtedy  nie posiada krawędzi wtórnej do żadnego z przodków
nie posiada krawędzi wtórnej do żadnego z przodków  , w takim razie
, w takim razie  jest punktem artykulacji (Twierdzenie B).
jest punktem artykulacji (Twierdzenie B).







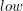 dla wszystkich wierzchołków. Inny natomiast jest krok trzeci, ale nie ma czym się martwić, gdyż jest on tak samo prosty jak przy szukaniu mostów.
dla wszystkich wierzchołków. Inny natomiast jest krok trzeci, ale nie ma czym się martwić, gdyż jest on tak samo prosty jak przy szukaniu mostów. nie będący korzeniem drzewa DFS jest punktem artykulacji wtedy i tylko wtedy, gdy przynajmniej dla jednego jego syna nie istnieje krawędź wtórna
nie będący korzeniem drzewa DFS jest punktem artykulacji wtedy i tylko wtedy, gdy przynajmniej dla jednego jego syna nie istnieje krawędź wtórna 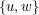 , taka że wierzchołek
, taka że wierzchołek  jest potomkiem
jest potomkiem 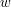 jest przodkiem
jest przodkiem  drzewa DFS ma mniej niż dwóch synów, to nie może być punktem artykulacji. Jeśli
drzewa DFS ma mniej niż dwóch synów, to nie może być punktem artykulacji. Jeśli 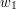 i
i 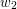 oraz
oraz 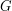 . Niech
. Niech 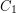 będzie spójną częścią grafu
będzie spójną częścią grafu  będzie sąsiadem
będzie sąsiadem 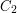 będzie spójną częścią grafu
będzie spójną częścią grafu ![$ low[s] \ge d[v] $](/files/tex/0cbd67a14f7c9d604a48782fee7237d0d78f0021.png) , wtedy
, wtedy 

