Mosty i punkty artykulacji
02.10.2010 - Michał Karpiński
  PrzykładSprawdźmy nasz nowo poznany algorytm w praktyce. W grafie przedstawionym na poniższej animacji znajdują się dwa punkty artykulacji. Korzystając z przedstawionych na poprzedniej stronie kroków postaramy się je znaleźć. Warto zauważyć, że graf składa się z trzech spójnych składowych, czyli po wykonaniu procedury DFS będziemy rozważali trzy różne drzewa. 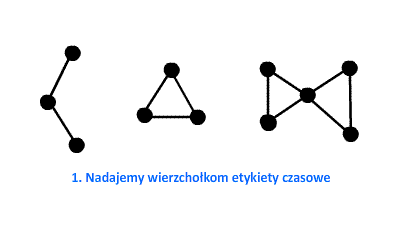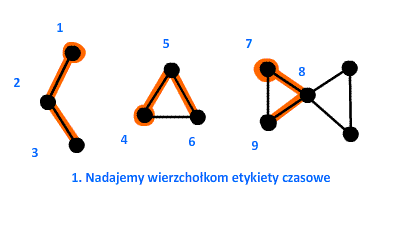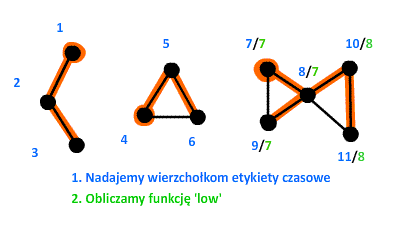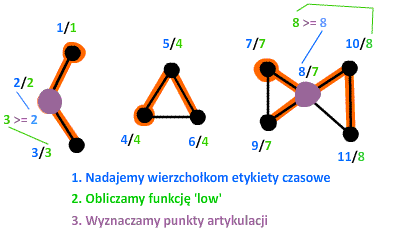 Łatwo też zauważyć, że w grafie znajdują się dwa mosty – każdy z nich połączony końcem z tym samym punktem artykulacji. W ramach ćwiczeń zastanów się, czy prawdą jest, że każdy most posiada na swoich końcach przynajmniej jeden punkt artykulacji. Narysuj kilka prostych przykładów. Złożoność czasowaW ostatnim rozdziale niniejszego artykułu odpowiemy na pytanie: ile czasu zajmie wykonanie algorytmu wyszukiwania mostów i punktów artykulacji w grafie nieskierowanym? Mówimy o ‘czasie‘ jako o pewnej ilości zasobu, który jest niezbędny do wykonania algorytmu, czyli ile operacji elementarnych należy wykonać na danych wejściowych, aby algorytm mógł się zakończyć. Złożoność czasowa zależna jest od rozmiaru danych wejściowych (choć nie zawsze). W naszym przypadku rozważać będziemy ilość wierzchołków ( 1. Na początek załóżmy, że graf wejściowy jest spójny. Wiemy, że procedura DFS działa w czasie 2. Sprawdźmy jak długo zajmie wyliczenie funkcji 3a. Przy szukaniu mostów trzeba ponownie przejrzeć każdy wierzchołek 3b. Przy szukaniu punktów artykulacji również trzeba przejrzeć z powrotem wszystkie wierzchołki. Znalezienie punktów artykulacji - z tego samego powodu co powyżej - zajmie (11 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


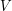 ) oraz ilość krawędzi (
) oraz ilość krawędzi (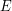 ) podanego grafu. Operacjami, którymi będziemy się posługiwali są przejścia z wierzchołka do jego sąsiada, przeglądnięcie listy sąsiedztwa itp. Będziemy korzystali z
) podanego grafu. Operacjami, którymi będziemy się posługiwali są przejścia z wierzchołka do jego sąsiada, przeglądnięcie listy sąsiedztwa itp. Będziemy korzystali z 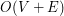 , ale gdy graf jest spójny, to
, ale gdy graf jest spójny, to 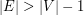 i wtedy złożoność czasowa wynosi
i wtedy złożoność czasowa wynosi 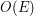 .
.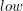 . Dla każdego wierzchołka
. Dla każdego wierzchołka  patrzymy na
patrzymy na ![$ d[v] $](/files/tex/115edd3c5063780310d2d9d18ef003a1d361c801.png) i na wszystkie krawędzie wychodzące z
i na wszystkie krawędzie wychodzące z ![$ low[v] = d[v] $](/files/tex/277b71999f8a52febdf02ee20796bc42c9236242.png) . Czyli trzeba wykonać
. Czyli trzeba wykonać 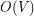 operacji. Wciąż trzeba mieć na uwadze, że
operacji. Wciąż trzeba mieć na uwadze, że 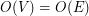 . Całkowity czas znalezienia mostów w grafie wynosi
. Całkowity czas znalezienia mostów w grafie wynosi 

