Mosty i punkty artykulacji
02.10.2010 - Michał Karpiński
  W poszukiwaniu mostówW tym rozdziale bajeczka o Bajtowie kończy się. Pora zająć się analizą problemu, któremu poświęcona jest pierwsza połowa tego artykułu. Nasze zadanie można sformułować w następujący sposób: Należy skonstruować algorytm, który dla podanego grafu nieskierowanego w krótkim czasie wyszuka w nim wszystkie mosty.Można spytać: dlaczego potrzebny jest nam taki algorytm? Odpowiedź jest prosta: żeby można było szybko wyszukiwać mosty dla dowolnie skomplikowanego grafu. W niektórych przypadkach znalezienie wszystkich mostów nie zajmie nawet minuty: 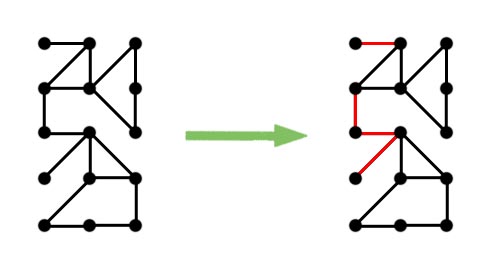 Na rysunku powyżej mosty zostały oznaczone na czerwono. Wyszukiwanie mostów w grafach o takim rozmiarze przypomina dziecinną zabawę. Jednak najczęściej graf wejściowy będzie znacznie większy i nie dość, że trudno będzie odnaleźć choć jeden most, to nie do końca będzie pewne, czy graf w ogóle takowe posiada. 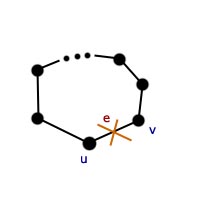
Rozpoczynamy analizę. Na początek dobrze jest wyodrębnić te krawędzie, które na pewno nie mogą być mostami. Po krótkim namyśle zapisujemy prostą obserwację: Krawędź Powyższe stwierdzenie jest bardzo prosto udowodnić. Skoro istnieje droga z Załóżmy, że nie usuwamy Jeśli krawędź z grafu |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


 łącząca wierzchołki
łącząca wierzchołki  i
i  nie może być mostem, jeśli po usunięciu
nie może być mostem, jeśli po usunięciu 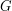 nie leży na żadnym cyklu prostym, to jest ona mostem.
nie leży na żadnym cyklu prostym, to jest ona mostem.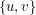 nie leży na żadnym cyklu prostym i nie jest ona mostem. Usuwamy krawędź
nie leży na żadnym cyklu prostym i nie jest ona mostem. Usuwamy krawędź 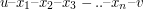 . A to oznacza, że
. A to oznacza, że 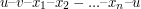 tworzy cykl prosty. Sprzeczność z założeniem, że
tworzy cykl prosty. Sprzeczność z założeniem, że 

