Otoczka wypukła
01.12.2011 - Michał Karpiński
  Znajdowanie otoczki wypukłej jest jednym z podstawowych problemów w geometrii obliczeniowej. Fakt, że w ciągu ostatnich 50 lat powstało bardzo wiele publikacji na temat tego zagadnienia świadczy o jego znaczeniu w dziedzinie algorytmiki. W niniejszym artykule zajmiemy się znajdowaniem otoczki wypukłej na płaszczyźnie. Można oczywiście rozważać przestrzeń trójwymiarową (lub jeszcze większą), lecz sformułowany w takich przestrzeniach problem i jego rozwiązanie zazwyczaj ciężko jest zobrazować. Mimo to wspomnimy o kilku algorytmach działających w trzech wymiarach, lecz nie będziemy się zbytnio w nie zagłębiać.Od razu zaczniemy od definicji, gdyż jest na tyle prosta i intuicyjna, że każdy powinien ją bez trudu zrozumieć: Otoczka wypukła (convex hull) zbioru punktów Otoczkę wypukłą w łatwy sposób można sobie wyobrazić. Załóżmy, że zamiast zbioru punktów mamy gwoździe, które są przybite w kilkunastu miejscach na jakiejś płaskiej powierzchni:  Weźmy teraz gumkę recepturkę, rozciągnijmy ją i nałóżmy na wszystkie wystające gwoździe: 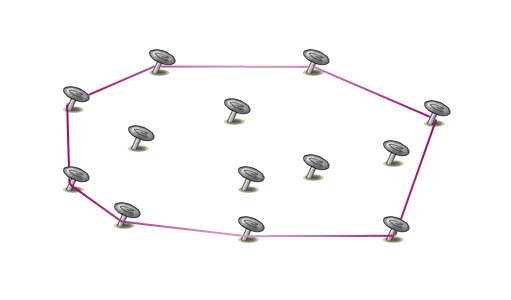 Gumka przyjęła kształt wielokąta wypukłego, a wszystkie gwoździe albo stykają się z gumką od wewnętrznej strony, albo znajdują się wewnątrz gumki. Tak ustawiona gumka jest otoczką wypukłą dla danego zbioru gwoździ. W kolejnej części artykułu zajmiemy się kilkoma popularnymi metodami znajdowania otoczki wypukłej na płaszczyźnie. Zapiszemy każdy z algorytmów w postaci pseudokodu oraz przeanalizujemy pod kątem złożoności czasowej. Zapraszam wszystkich zainteresowanych do lektury. Metoda pakowania prezentuPakowanie prezentu jest jedną z najprostszych metod znajdowania otoczki wypukłej (alternatywnie można też na nią mówić algorytm Jarvisa, od nazwiska matematyka, który ją wymyślił). Niejednego pewnie zastanawia skąd wziął się taki dziwny pomysł na nazwanie algorytmu? Wszystkie wątpliwości powinna wyjaśnić poniższa animacja:  Algorytm Jarvisa można intuicyjnie opisać w następujący sposób: jeśli popatrzymy na czerwoną półprostą jako na kawałek papieru, to algorytm opakowuje ciasno cały zbiór punktów. Zaczynamy od zamocowania jednego końca taśmy papierowej do najbardziej wysuniętego na prawo punktu. Następnie owijamy wszystkie punkty dookoła. Kończymy owijanie, gdy wrócimy do miejsca, z którego zaczynaliśmy. Widzimy „na oko”, że to działa. Wielokąt wypukły, który powstanie po opakowaniu wszystkich punktów faktycznie jest ich otoczką wypukłą. Dowody „na wiarę” nie są jednak zbyt fascynujące, dlatego powinniśmy przedstawić jakiś konkretny argument przemawiający za poprawnością nowo poznanej metody.
(5 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


 to najmniejszy wielokąt wypukły taki, że każdy punkt ze zbioru
to najmniejszy wielokąt wypukły taki, że każdy punkt ze zbioru 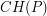 .
.

