Otoczka wypukła
01.12.2011 - Michał Karpiński
  Inne metodyDo tej pory poznaliśmy dwa algorytmy wyznaczające otoczkę wypukłą na płaszczyźnie i dokładnie je omówiliśmy. Ponadto dokonaliśmy analizy złożoności i udowodniliśmy ich poprawność. Nie musimy się jednak ograniczać tylko do tych dwóch metod. Jak wspomniałem we wstępie, nad problemem otoczki wypukłej pracowało (i dalej pracuje) wielu informatyków. W ciągu kilkudziesięciu lat powstało mnóstwo różnych algorytmów rozwiązujący ten problem. W tym rozdziale chciałbym przedstawić kilka metod, które pokazują różne podejścia do szukania otoczki. Nie będziemy się wgłębiali zbytnio w te algorytmy. Przedstawiona zostanie tylko ich idea. Zachęcam do przeprowadzenia własnych eksperymentów i badań. Incremental - metoda przyrostowaMetoda przyrostowa pokazuje naturalne podejście do rozwiązania problemu otoczki. Wynik będziemy przechowywali na liście podwójnie łączonej (nazwiemy ją oczywiście Najpierw dodajemy do 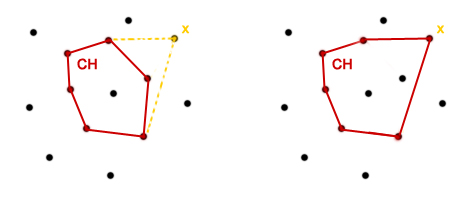 Nietrudno zauważyć, że po Poprawność dowodzimy przez prostą indukcję, więc szczegóły pominiemy. Niestety ta metoda nie jest zbyt efektywna. Jej złożoność to Dziel i zwyciężajJeśli znamy algorytm sortowania przez scalanie, to nie będziemy mieli problemu ze zrozumieniem działania algorytmów wyznaczania otoczki wypukłej metodą dziel i zwyciężaj, gdyż w obu przypadkach schemat jest ten sam: rozbijamy problem na dwa pod-problemy, pod-problemy rozwiązujemy rekurencyjnie i rozwiązania pod-problemów scalamy w jedną całość. Ogólną procedurę można by zapisać w taki sposób:  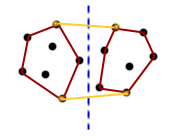
Pozostają pytania: jak dzielić? Jak scalać? Najbardziej intuicyjne byłoby wyznaczenie pionowej prostej dzielącej zbiór Zauważmy, że dzielenie można zrobić w czasie stałym. Wystarczy wcześniej posortować zbiór Można spróbować innego podejścia. Załóżmy, że nie chcemy sortować zbioru 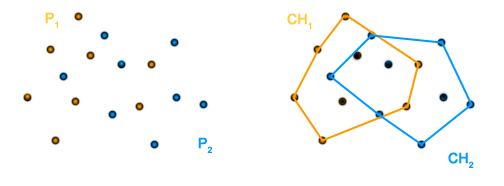 Problem ten można sprytnie rozwiązać: weźmy dowolny punkt leżący wewnątrz otoczki 1. Punkt 2. Punkt 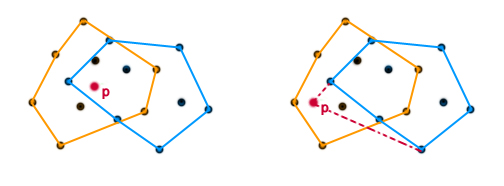 Która metoda dzielenia i scalania wydaje się być prostsza? To już zależy od osobistych preferencji. W każdym razie złożoność czasowa i tak się nie zmienia. W obu przypadkach wynosi (5 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


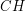 ). Idea algorytmu jest taka:
). Idea algorytmu jest taka: . Następnie iterujemy po zbiorze
. Następnie iterujemy po zbiorze ![$ P[3..n] $](/files/tex/03fa5f1704efe5ec79a5fc7f7a8976c9fee27814.png) . Dla każdego punktu
. Dla każdego punktu  ze zbioru
ze zbioru  -tej iteracji
-tej iteracji ![$ P[1..i] $](/files/tex/efb6fe106e635311488fd0f969c7269e3bb339a2.png) . Każdy nowy punkt po prostu "doczepiamy" do otoczki. Stąd wzięła się nazwa algorytmu, bo otoczka się tak jakby "rozrasta".
. Każdy nowy punkt po prostu "doczepiamy" do otoczki. Stąd wzięła się nazwa algorytmu, bo otoczka się tak jakby "rozrasta".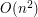 z uwagi na to, że dla każdego punktu z
z uwagi na to, że dla każdego punktu z 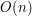 , ale to zadnie pozostawię czytelnikowi jako ćwiczenie.
, ale to zadnie pozostawię czytelnikowi jako ćwiczenie.![$ P[1..\lfloor \frac{n}{2} \rfloor] $](/files/tex/3e45938cfad0b6961038a3685259885a541ed5e0.png) i
i ![$ P[\lceil \frac{n}{2} \rceil ..n] $](/files/tex/291ff047c4451128ca2369c50c7054be0ea8bbb2.png) . Na tych podzbiorach rekurencyjnie szukamy otoczki. Krok scalania będzie jednak bardziej skomplikowany, gdyż otoczki
. Na tych podzbiorach rekurencyjnie szukamy otoczki. Krok scalania będzie jednak bardziej skomplikowany, gdyż otoczki 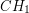 i
i 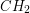 nie muszą być rozłączne (czyli mogą na siebie zachodzić).
nie muszą być rozłączne (czyli mogą na siebie zachodzić). . Sprawdzamy, czy punkt
. Sprawdzamy, czy punkt 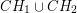 , który jest posortowany względem
, który jest posortowany względem 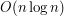 .
.

