Algorytm Grahama cd.
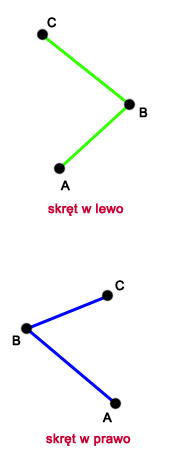
Otoczkę wypukłą będziemy budowali w kierunku odwrotnym do ruchu wskazówek zegara. Zauważmy, że jeśli weźmiemy gotową otoczkę wypukłą, wyszczególnimy jakikolwiek jej punkt i przejdziemy po całej otoczce w kierunku odwrotnym do ruchu wskazówek zegara, to każde trzy kolejne punkty będą tworzyły tzw. skręt w lewo (patrz rysunek obok). W algorytmie Grahama korzystamy właśnie z tego faktu. Zauważmy też, że skręt w lewo (lub prawo) można łatwo wykryć w czasie stałym korzystając ze znanej już procedury 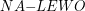 .
.
Kolejnych kandydatów na otoczkę wypukłą będziemy umieszczali na pomocniczym stosie 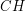 . Po zakończeniu działania algorytmu w
. Po zakończeniu działania algorytmu w 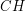 będą się znajdowały kolejne punkty otoczki. Ogólną ideę działania algorytmu można opisać w następujący sposób:
będą się znajdowały kolejne punkty otoczki. Ogólną ideę działania algorytmu można opisać w następujący sposób:
1. Pierwsze dwa punkty ze zbioru ![$ P[1..n] $](/files/tex/c5086e0dcd31c9348ba95f854c1e228de6a375ef.png) umieszczamy na stosie (pamiętamy, że tablica
umieszczamy na stosie (pamiętamy, że tablica  jest już posortowana )
jest już posortowana )
2. Układamy kolejne punkty ze zbioru  na stosie
na stosie 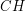 dopóki tworzą - wraz z dwoma elementami na szczycie stosu - skręt w lewo.
dopóki tworzą - wraz z dwoma elementami na szczycie stosu - skręt w lewo.
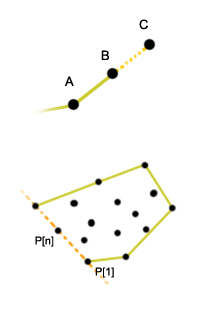
3. Jeśli doszliśmy do punktu startowego, algorytm się kończy. W przeciwnym razie napotkaliśmy miejsce, gdzie kolejny punkt z  wraz z dwoma elementami na szczycie stosu tworzą skręt w prawo. Nazwijmy te punkty kolejno
wraz z dwoma elementami na szczycie stosu tworzą skręt w prawo. Nazwijmy te punkty kolejno  ,
,  , i
, i  (patrz rysunek obok; niebieskie krawędzie).
(patrz rysunek obok; niebieskie krawędzie).  i
i  leżą na stosie, a
leżą na stosie, a  jest kolejnym punktem z
jest kolejnym punktem z  . Widać, że w takim wypadku punkt
. Widać, że w takim wypadku punkt  na pewno nie będzie należał do otoczki. Może być kuszące, aby połączyć po prostu punkt
na pewno nie będzie należał do otoczki. Może być kuszące, aby połączyć po prostu punkt  z
z  , ale niestety nie jest to poprawne podejście. Mianowicie, może się okazać, że następny element ze stosu (znajdujący się poniżej
, ale niestety nie jest to poprawne podejście. Mianowicie, może się okazać, że następny element ze stosu (znajdujący się poniżej  ) po połączeniu z
) po połączeniu z  wykluczy
wykluczy  z bycia częścią otoczki. Może to też być jakiś inny element ze stosu. Co należy zrobić, to usuwać ze stosu kolejne elementy dopóki nie będzie spełniony warunek skrętu w lewo. Przykład "naprawienia własności skrętu w lewo" demonstruje poniższa animacja:
z bycia częścią otoczki. Może to też być jakiś inny element ze stosu. Co należy zrobić, to usuwać ze stosu kolejne elementy dopóki nie będzie spełniony warunek skrętu w lewo. Przykład "naprawienia własności skrętu w lewo" demonstruje poniższa animacja:
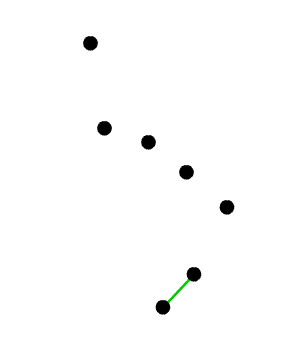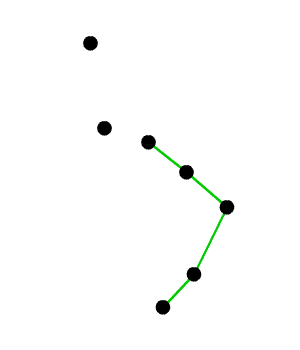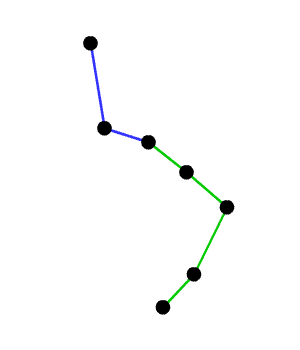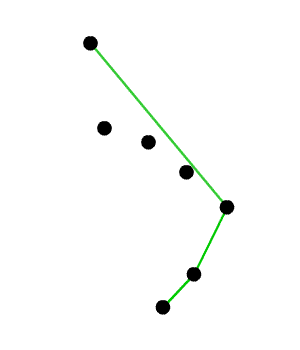
Posiadamy już dostateczną wiedzę, aby zapisać algorytm Grahama w postaci pseudokodu:

Dowód poprawności
Dowodzimy poprawności algorytmu Grahama stosując prostą indukcję przy użyciu następującego niezmiennika pętli zewnętrznej:
Po  -tej iteracji pętli zewnętrznej punkty
-tej iteracji pętli zewnętrznej punkty ![$ P[1..i] $](/files/tex/efb6fe106e635311488fd0f969c7269e3bb339a2.png) są przetworzone tak, że część z nich należy do stosu
są przetworzone tak, że część z nich należy do stosu 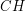 , a część nie. Te z nich, które należą do stosu
, a część nie. Te z nich, które należą do stosu 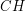 tworzą kolejno łańcuch krawędzi taki, że dla każdej krawędzi, wszystkie inne punkty nienależące do
tworzą kolejno łańcuch krawędzi taki, że dla każdej krawędzi, wszystkie inne punkty nienależące do  (a będące w
(a będące w ![$ P[1..i] $](/files/tex/efb6fe106e635311488fd0f969c7269e3bb339a2.png) ) znajdują się na lewo od niej.
) znajdują się na lewo od niej.
Przed pierwszą iteracją niezmiennik jest zachowany w trywialny sposób. Załóżmy teraz, że jesteśmy po  -tej iteracji i przystępujemy do iteracji
-tej iteracji i przystępujemy do iteracji 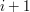 -szej. Zauważmy, że jeśli punkt
-szej. Zauważmy, że jeśli punkt ![$ P[i+1] $](/files/tex/fb8848ed90bdcfc85f70f37e8524ae9834e5a22f.png) psuje własność "skrętu w lewo", to pętla wewnętrzna nam to naprawi. Przy okazji wszystkie punkty, które odrzuci będą znajdowały się na lewo od nowo utworzonej krawędzi. Niezmiennik zostaje zachowany. Gdy pętla się skończy w
psuje własność "skrętu w lewo", to pętla wewnętrzna nam to naprawi. Przy okazji wszystkie punkty, które odrzuci będą znajdowały się na lewo od nowo utworzonej krawędzi. Niezmiennik zostaje zachowany. Gdy pętla się skończy w 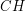 znajdą się kolejne punkty otoczki wypukłej (na mocy twierdzenia, które udowodniliśmy przy omawianiu algorytmu Jarvisa).
znajdą się kolejne punkty otoczki wypukłej (na mocy twierdzenia, które udowodniliśmy przy omawianiu algorytmu Jarvisa).
Analiza złożoności
Nie uwzględniając czasu sortowania mogłoby się wydawać, że algorytm Grahama działa w czasie 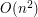 , gdyż zewnętrzna pętla wykonuje się
, gdyż zewnętrzna pętla wykonuje się 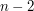 razy, a wewnętrzna pętla może przejść po całym stosie
razy, a wewnętrzna pętla może przejść po całym stosie 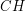 (który maksymalnie może zawierać
(który maksymalnie może zawierać  elementów). Zauważmy jednak, że każdy punkt ze zbioru
elementów). Zauważmy jednak, że każdy punkt ze zbioru  rozpatrujemy co najwyżej dwa razy - raz gdy zostaje dodany do stosu i raz gdy zostaje usunięty z niego (nie licząc momentów, w których podglądamy wartości dwóch górnych elementów stosu do określenia "skrętu"). Z tego wynika, że właściwa część szukania otoczki wypukłej wykonuje się w czasie
rozpatrujemy co najwyżej dwa razy - raz gdy zostaje dodany do stosu i raz gdy zostaje usunięty z niego (nie licząc momentów, w których podglądamy wartości dwóch górnych elementów stosu do określenia "skrętu"). Z tego wynika, że właściwa część szukania otoczki wypukłej wykonuje się w czasie 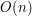 . Jeśli dodamy do tego czas na posortowanie tablicy
. Jeśli dodamy do tego czas na posortowanie tablicy  , to ogólna złożoność wynosi
, to ogólna złożoność wynosi 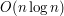 .
.
Przypadki zdegenerowane
Jeśli chodzi o algorytm Grahama, to musimy rozpatrzyć taką samą kwestię, jak przy metodzie pakowania prezentu. Chodzi oczywiście o sytuację, gdy trzy punkty są współliniowe. Problem nietrudno jest rozwiązać dodając odpowiedni warunek do pętli wewnętrznej. Popatrzmy na rysunek. Jeśli punkt  jest współliniowy z
jest współliniowy z  i
i  (i znajduje się dalej od
(i znajduje się dalej od  ), to
), to  usuwamy, a
usuwamy, a  dodajemy do stosu.
dodajemy do stosu.
Jednak tutaj należy również pamiętać o jednym skrajnym przypadku. Gdy algorytm się skończy może się okazać, że dwa ostatnio dodane punkty do stosu i punkt startowy są współliniowe (warunek w pętli wewnętrznej tego nie wykryje, bo ostatni rozpatrywany punkt to ![$ P[n] $](/files/tex/ef469e17ab44298036476368eca0fc18121d72fc.png) – nie porównujemy go z
– nie porównujemy go z ![$ P[1] $](/files/tex/d9fd1aa6642943d9de4d3a462e49bc6c5c5ca796.png) ). Po skończeniu działania pętli zewnętrznej należy porównać punkt
). Po skończeniu działania pętli zewnętrznej należy porównać punkt ![$ P[1] $](/files/tex/d9fd1aa6642943d9de4d3a462e49bc6c5c5ca796.png) z dwoma ostatnimi elementami
z dwoma ostatnimi elementami 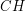 i ostatni element z
i ostatni element z 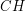 ewentualnie usunąć.
ewentualnie usunąć.








 .
. . Po zakończeniu działania algorytmu w
. Po zakończeniu działania algorytmu w ![$ P[1..n] $](/files/tex/c5086e0dcd31c9348ba95f854c1e228de6a375ef.png) umieszczamy na stosie (pamiętamy, że tablica
umieszczamy na stosie (pamiętamy, że tablica  jest już posortowana )
jest już posortowana ) ,
,  , i
, i  (patrz rysunek obok; niebieskie krawędzie).
(patrz rysunek obok; niebieskie krawędzie).  -tej iteracji pętli zewnętrznej punkty
-tej iteracji pętli zewnętrznej punkty ![$ P[1..i] $](/files/tex/efb6fe106e635311488fd0f969c7269e3bb339a2.png) są przetworzone tak, że część z nich należy do stosu
są przetworzone tak, że część z nich należy do stosu 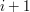 -szej. Zauważmy, że jeśli punkt
-szej. Zauważmy, że jeśli punkt ![$ P[i+1] $](/files/tex/fb8848ed90bdcfc85f70f37e8524ae9834e5a22f.png) psuje własność "skrętu w lewo", to pętla wewnętrzna nam to naprawi. Przy okazji wszystkie punkty, które odrzuci będą znajdowały się na lewo od nowo utworzonej krawędzi. Niezmiennik zostaje zachowany. Gdy pętla się skończy w
psuje własność "skrętu w lewo", to pętla wewnętrzna nam to naprawi. Przy okazji wszystkie punkty, które odrzuci będą znajdowały się na lewo od nowo utworzonej krawędzi. Niezmiennik zostaje zachowany. Gdy pętla się skończy w 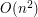 , gdyż zewnętrzna pętla wykonuje się
, gdyż zewnętrzna pętla wykonuje się 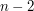 razy, a wewnętrzna pętla może przejść po całym stosie
razy, a wewnętrzna pętla może przejść po całym stosie  elementów). Zauważmy jednak, że każdy punkt ze zbioru
elementów). Zauważmy jednak, że każdy punkt ze zbioru 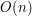 . Jeśli dodamy do tego czas na posortowanie tablicy
. Jeśli dodamy do tego czas na posortowanie tablicy 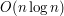 .
.![$ P[n] $](/files/tex/ef469e17ab44298036476368eca0fc18121d72fc.png) – nie porównujemy go z
– nie porównujemy go z ![$ P[1] $](/files/tex/d9fd1aa6642943d9de4d3a462e49bc6c5c5ca796.png) ). Po skończeniu działania pętli zewnętrznej należy porównać punkt
). Po skończeniu działania pętli zewnętrznej należy porównać punkt 

