Metoda pakowania prezentu cd.
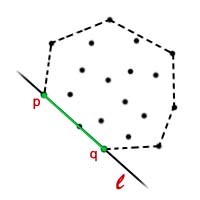
Mamy dany zbiór punktów  . Zamiast patrzeć na całą otoczkę spójrzmy jedynie na którąkolwiek z krawędzi, która do niej należy. Taka krawędź łączy dwa punkty, które nazwiemy
. Zamiast patrzeć na całą otoczkę spójrzmy jedynie na którąkolwiek z krawędzi, która do niej należy. Taka krawędź łączy dwa punkty, które nazwiemy  i
i 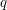 . Łatwo jest dostrzec, że wszystkie inne punkty ze zbioru
. Łatwo jest dostrzec, że wszystkie inne punkty ze zbioru  muszą: albo leżeć na krawędzi
muszą: albo leżeć na krawędzi 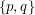 , albo znajdować się po jednej stronie prostej
, albo znajdować się po jednej stronie prostej 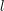 , którą wyznaczają punkty
, którą wyznaczają punkty  i
i 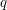 . Twierdzenie odwrotne również zachodzi. Podsumowując:
. Twierdzenie odwrotne również zachodzi. Podsumowując:
Krawędź 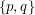 należy do otoczki wypukłej wtedy i tylko wtedy, gdy wszystkie inne punkty leżą na lub po jednej ze stron tej krawędzi.
należy do otoczki wypukłej wtedy i tylko wtedy, gdy wszystkie inne punkty leżą na lub po jednej ze stron tej krawędzi.
Teraz widać, że pakowanie prezentu rzeczywiście wyznacza otoczkę wypukłą, gdyż kolejne krawędzie dołączane do otoczki spełniają powyższy warunek.
Pseudokod
Pora przedstawić procedurę, która odwzorowuję naszą intuicję o pakowaniu prezentu. Nie będziemy jednak fizycznie tworzyli półprostej obracającej się wokół własnej osi. Takie podejście jest nieefektywne i niepoprawne. „Pakowanie” to tylko sposób myślenia o rozwiązaniu naszego problemu. W rzeczywistości do odkrywania kolejnych punktów otoczki posłużymy się twierdzeniem z poprzedniego akapitu. Przeanalizujmy poniższy algorytm:

Oto znaczenie zmiennych i struktur użytych w procedurze 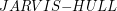 :
:
![$ P[1..n] $](/files/tex/c5086e0dcd31c9348ba95f854c1e228de6a375ef.png) – tablica punktów płaszczyzny podanych na wejściu
– tablica punktów płaszczyzny podanych na wejściu![$ CH[1..n] $](/files/tex/b8f88e62d6d37a1e98f98fdf9e75be391f9abce6.png) – tablica, w której przechowywane są kolejne punkty należące do otoczki wypukłej. Wielkość tej tablicy to
– tablica, w której przechowywane są kolejne punkty należące do otoczki wypukłej. Wielkość tej tablicy to  , ponieważ może się zdarzyć, że każdy punkt z
, ponieważ może się zdarzyć, że każdy punkt z  należy do otoczki (w większości przypadków będzie ich znacznie mniej).
należy do otoczki (w większości przypadków będzie ich znacznie mniej).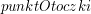 – jest to zmienna przechowująca punkt, który na pewno znajdzie się w otoczce.
– jest to zmienna przechowująca punkt, który na pewno znajdzie się w otoczce.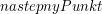 – zmienna pomocnicza, która przechowuje kandydatów na kolejny punkt otoczki
– zmienna pomocnicza, która przechowuje kandydatów na kolejny punkt otoczki
Algorytm działa następująco:
1. Wyznaczamy punkt startowy. Jest to taki punkt ze zbioru  , który na pewno znajdzie się w rozwiązaniu. Nie ma chyba żadnych wątpliwości, że punkt, który znajduje się najbardziej na prawo spełnia nasze założenia. Przypisujemy ten punkt do zmiennej
, który na pewno znajdzie się w rozwiązaniu. Nie ma chyba żadnych wątpliwości, że punkt, który znajduje się najbardziej na prawo spełnia nasze założenia. Przypisujemy ten punkt do zmiennej 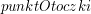 . Kolejnych punktów otoczki będziemy szukali zgodnie z ruchem wskazówek zegara.
. Kolejnych punktów otoczki będziemy szukali zgodnie z ruchem wskazówek zegara.
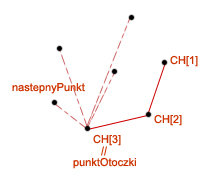
2. Wchodzimy w pętle zewnętrzną. Dodajemy znaleziony punkt otoczki do rozwiązania.
3. Szukamy następnego punktu otoczki, który będziemy przechowywać w zmiennej 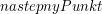 . Teraz najważniejsze: chcemy, aby kolejny punkt wraz z ostatnio znalezionym punktem otoczki utworzyli krawędź skierowaną
. Teraz najważniejsze: chcemy, aby kolejny punkt wraz z ostatnio znalezionym punktem otoczki utworzyli krawędź skierowaną ![$ \{ CH[i], nastepnyPunkt \} $](/files/tex/044dbb6f8f34690be7eab2d545b599cae70a8b7a.png) taką, że wszystkie inne punkty ze zbioru
taką, że wszystkie inne punkty ze zbioru  leżą na prawo od niej.
Taki punkt można wyznaczyć w bardzo prosty sposób. Najpierw do zmiennej
leżą na prawo od niej.
Taki punkt można wyznaczyć w bardzo prosty sposób. Najpierw do zmiennej 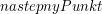 przypisujemy pierwszy element zbioru
przypisujemy pierwszy element zbioru  . W pętli wewnętrznej sprawdzamy kolejne elementy zbioru
. W pętli wewnętrznej sprawdzamy kolejne elementy zbioru  . Jeśli zdarzy się, że w
. Jeśli zdarzy się, że w  -tej iteracji punkt
-tej iteracji punkt ![$ P[j] $](/files/tex/3f323be402bcb2bf644443d98bbc24ad25a40c28.png) znajduje się na lewo od krawędzi
znajduje się na lewo od krawędzi ![$ \{ CH[i], nastepnyPunkt \} $](/files/tex/044dbb6f8f34690be7eab2d545b599cae70a8b7a.png) , to aktualizujemy zmienną
, to aktualizujemy zmienną 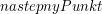 przypisując jej nową wartość:
przypisując jej nową wartość: ![$ P[j] $](/files/tex/3f323be402bcb2bf644443d98bbc24ad25a40c28.png) . Aby wykonać tego sprawdzenia posłużymy się pomocniczą procedurą
. Aby wykonać tego sprawdzenia posłużymy się pomocniczą procedurą 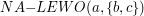 , która wyznacza, po której stronie krawędzi
, która wyznacza, po której stronie krawędzi 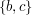 znajduje się punkt
znajduje się punkt  . Po opuszczeniu pętli w zmiennej
. Po opuszczeniu pętli w zmiennej 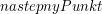 znajdować się będzie kolejny punkt należący do otoczki wypukłej. Wartość tą przypisujemy zmiennej
znajdować się będzie kolejny punkt należący do otoczki wypukłej. Wartość tą przypisujemy zmiennej 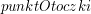 .
.
Mała dygresja: warto zauważyć, że wyznaczenie kolejnego punktu otoczki jest bardzo podobne do szukania największego elementu ze zbioru liczb. Najpierw przyjmujemy, że największym element jest pierwszy ze zbioru. Następnie przechodzimy od lewej do prawej cały zbiór i aktualizujemy naszego "maxa", jeśli któryś z elementów jest od niego większy. W algorytmie Jarvisa zbiór liczb zamieniamy na zbiór punktów, a relację "mniejszy-równy" na relację "na-lewo-od".
4. Jeśli następny punkt otoczki jest za razem pierwszym, to algorytm się kończy. W przeciwnym razie wracamy do kroku 2.
Poprawność algorytmu wynika wprost z udowodnionego wcześniej twierdzenia.
O procedurze NA-LEWO
W naszym algorytmie wykorzystaliśmy pomocniczą funkcję 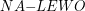 , która dla danego punktu i skierowanego odcinka sprawdzała, po której stronie odcinka leży ten punkt. Oto definicja tej funkcji:
, która dla danego punktu i skierowanego odcinka sprawdzała, po której stronie odcinka leży ten punkt. Oto definicja tej funkcji:
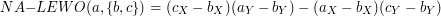
Jeśli zwrócona wartość jest:
- większa od zera, to punkt
 leży na lewo od odcinka
leży na lewo od odcinka 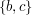
- mniejsza od zera, to punkt
 leży na prawo od odcinka
leży na prawo od odcinka 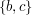
- równa zero. Oznacza to, że punkty
 ,
,  oraz
oraz  są współliniowe (czyli leżą na jednej prostej). Ten przypadek omówimy osobno na następnej stronie.
są współliniowe (czyli leżą na jednej prostej). Ten przypadek omówimy osobno na następnej stronie.
Mała uwaga: jeśli nie jesteś do końca przekonany, że powyższy wzór jest poprawny, to polecam przeczytanie artykułu pt. "Krótki wstęp do algorytmów geometrycznych".
Złożoność czasowa
Algorytm Jarvisa jest na tyle prosty, że nie będziemy mieli problemów z analizą jego złożoności. Zauważmy, że wewnętrzna pętla przebiega po wszystkich  punktach, a zewnętrzna pętla wykona się dokładnie tyle razy, ile punktów leży na otoczce wypukłej. Podsumowując, jeśli oznaczymy liczbę punktów otoczki jako
punktach, a zewnętrzna pętla wykona się dokładnie tyle razy, ile punktów leży na otoczce wypukłej. Podsumowując, jeśli oznaczymy liczbę punktów otoczki jako 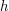 , to dokładnie
, to dokładnie 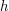 razy będziemy musieli przejrzeć tablicę rozmiaru
razy będziemy musieli przejrzeć tablicę rozmiaru  . Z tego wniosek, że złożoność czasowa algorytmu pakowania prezentu to
. Z tego wniosek, że złożoność czasowa algorytmu pakowania prezentu to 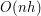 .
.
Zwróćmy uwagę na to, że czas jest zależny od wyniku. Nie jesteśmy w stanie przewidzieć wartości 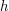 przed uruchomieniem procedury
przed uruchomieniem procedury 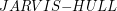 , chociaż w niektórych przypadkach można dokonać pewnych oszacowań, ale to już zależy od rozwiązywanego problemu. Czy warto więc stosować algorytm Jarvisa? Na pewno wielką zaletą jest jego prosta idea i łatwość implementacji. Należy jednak pamiętać, że dla pewnych złośliwych danych (np. gdy wszystkie punkty leżą na obwodzie koła) czas działania może wynieść nawet
, chociaż w niektórych przypadkach można dokonać pewnych oszacowań, ale to już zależy od rozwiązywanego problemu. Czy warto więc stosować algorytm Jarvisa? Na pewno wielką zaletą jest jego prosta idea i łatwość implementacji. Należy jednak pamiętać, że dla pewnych złośliwych danych (np. gdy wszystkie punkty leżą na obwodzie koła) czas działania może wynieść nawet 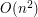 .
.





