Drzewce
03.10.2010 - Michał Karpiński
   Drzewa zrównoważone to niezwykle przydatne struktury danych. Można ich użyć np. do tworzenia słowników, w których kluczowym jest wykonywanie wszystkich operacji w jak najlepszym czasie. Strukturą, którą będziemy się zajmowali w niniejszym artykule jest drzewiec (z ang. treap), który łączy w sobie cechy binarnego drzewa przeszukiwań i kopca (również binarnego). Jeśli nie wiesz, czym są drzewa przeszukiwań binarnych, zapraszam do lektury tego artykułu na ich temat. Nazwa „drzewiec” bierze się z połączenia słowa „drzewo” (tree) i słowa „kopiec” (heap): drzewo + kopiec = drzewiec (tree + heap = treap). Nie bez powodu właśnie taką nazwę przyjęła ta drzewiasta struktura. Gdy mówimy o operacjach słownikowych, mamy na myśli wstawienie, usunięcie oraz odnalezienie klucza w danym zbiorze. Wiadomo, że te oparcje można z powodzeniem wykonywać na samym tylko drzewie BST. Skąd więc bierze się potrzeba do wprowadzenia jakichkolwiek zmian? Spójrzmy na poniższy rysunek. 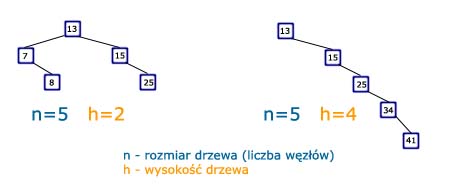
Bardziej szczegółową analizę drzew BST i operacji z nimi związanych można znaleźć w tym artykule Od razu widzimy różnicę pomiędzy tymi dwoma drzewami binarnymi. W pierwszym z nich aby wyszukać dowolny element trzeba użyć co najwyżej 3 operacje porównania. W drugim drzewie porównań wykonamy maksymalnie 5, mimo że oba drzewa mają taką samą ilość elementów. Oczywistym jest fakt, że wszystkie operacje słownikowe na drzewie BST wykonają się w czasie liniowo proporcjonalnym do jego wysokości, czyli Złożoność Więcej na temat kopców binarnych można przeczytać w tym artykule W osiągnięciu tego celu pomoże nam kopiec binarny, a dokładniej mówiąc: własność kopca. Własność kopca (typu max) mówi, że wartość danego węzła ma być większa od wartości jego synów. Skorzystamy z tej własności i zaaplikujemy ją do drzewa BST. Jednak jest pewien problem: w drzewie BST klucze w węzłach muszą spełniać inną własność, mianowicie taką, że lewy syn ma mieć wartość mniejszą, a prawy syn większą od wartości danego węzła. Nie możemy tak po prostu tego zburzyć. Na szczęście nic nie stoi na przeszkodzie, aby dodać do każdego węzła nowy atrybut zwany priorytetem, który możemy zastosować do utrzymywania w drzewie BST własności kopca. 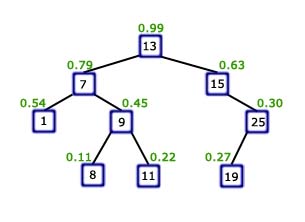
Dla uproszczenia przyjmiemy, że priorytety przyjmują wartości od 0 do 1 Na rysunku powyżej widać doskonały przykład drzewca. Kolejność kluczy jest zachowana w porządku zgodnym z drzewem BST oraz priorytety spełniają własność kopca typu max. Jednak czy tak skonstruowana struktura wystarczy aby szybko wykonywać operację słownikowe? Przecież łatwo jest podać przykład drzewca, który przypomina listę łączoną. Cały sekret drzewców polega na wyborze priorytetów. Otóż dla każdego nowego węzła - podczas wstawiania go do drzewa - priorytet jest wybierany CAŁKOWICIE LOSOWO, co (jak się niedługo przekonamy) sprawia, że - z dużym prawdopodobieństwem - wysokość drzewa przyjmuje wartość bliską
(2 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


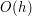 . Najgorszy jest przypadek pokazany na rysunku powyżej (z prawej strony), gdzie struktura bardziej przypomina listę łączoną niż drzewo binarne. W tym przypadku
. Najgorszy jest przypadek pokazany na rysunku powyżej (z prawej strony), gdzie struktura bardziej przypomina listę łączoną niż drzewo binarne. W tym przypadku 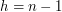 , co w znaczny sposób pogarsza złożoność czasową interesujących nas algorytmów.
, co w znaczny sposób pogarsza złożoność czasową interesujących nas algorytmów.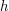 - z dużym prawdopodobieństwem - przyjmie jakąś sensowną wartość (np.
- z dużym prawdopodobieństwem - przyjmie jakąś sensowną wartość (np. 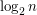 ), to posiadać będziemy wystarczające zasoby do zbudowania efektywnego słownika.
), to posiadać będziemy wystarczające zasoby do zbudowania efektywnego słownika.

