Drzewce
03.10.2010 - Michał Karpiński
   Procedura "Delete"Usuwanie elementu z drzewca można podzielić na trzy kroki:
Przy usuwaniu elementów - podobnie jak przy wstawianiu - dużą rolę odgrywają rotacje. Jednak zamiast wykonywać rotację na elemencie Problemu nie ma, jeśli dany wierzchołek ma tylko jednego syna. Wtedy w zależności czy jest to prawy czy lewy syn wykonujemy odpowiednio lewą albo prawą rotację. Syna Aby wszystko było jasne, prześledźmy prosty przykład: 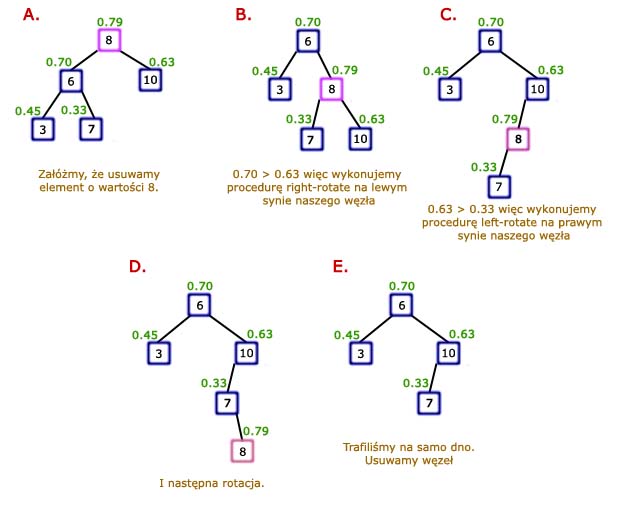
Poniżej przedstawiona jest procedura 
Podana procedura usuwania może na pierwszy rzut oka wydawać się skomplikowana. Jest tak dlatego, że podczas wykonywania pętli Pierwsza linijka procedury Drugi krok przeprowadzamy w pętli Usunięcie elementu polega jedynie na przestawieniu jednego wskaźnika i następuje po wyjściu z pętli, czyli gdy dany wierzchołek stał się liściem. Tutaj też musimy rozpatrzeć kilka przypadków. W szczególności trzeba pamiętać, że usuwany węzeł może być korzeniem. Uwaga: przy implementacji procedury usuwania za pomocą niskopoziomowego języka (np. C) należy pamiętać o zwolnieniu pamięci, w której zapisany był Najważniejsze: nie należy się zniechęcać. Wystarczy kilka minut przestudiować dokładnie powyższy pseudokod i wszystko stanie się jasne. Zachęcam do przetestowania procedur wstawiania i usuwania na własnych przykładach. (2 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com



 , (co sprawiłoby, że
, (co sprawiłoby, że 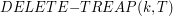 , która usuwa element o kluczu
, która usuwa element o kluczu 
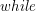 - w której przechodzimy z danym węzłem w dół przy pomocy rotacji - należy sprawdzić dużo przypadków.
- w której przechodzimy z danym węzłem w dół przy pomocy rotacji - należy sprawdzić dużo przypadków.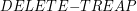 reprezentuje pierwszy krok usuwania podany na początku tego rozdziału i jest prosta do rozszyfrowania: najpierw szukamy czy element, który chcemy usunąć w ogóle znajduje się w drzewcu. Resztę algorytmu wykonujemy tylko, jeśli szukany element istnieje.
reprezentuje pierwszy krok usuwania podany na początku tego rozdziału i jest prosta do rozszyfrowania: najpierw szukamy czy element, który chcemy usunąć w ogóle znajduje się w drzewcu. Resztę algorytmu wykonujemy tylko, jeśli szukany element istnieje.

