Drzewa przeszukiwań binarnych
14.12.2009 - Michał Karpiński
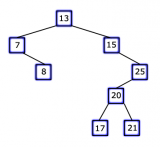
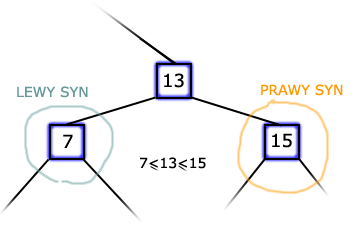
 skrócie BST (ang. binary search tree), jak sama nazwa wskazuje, ma strukturę drzewa binarnego. Tego typu drzewa stosuje się do szybkiego wyszukiwania jak również do realizacji bardziej abstrakcyjnych struktur danych. Uważam, że każda osoba chcąca zgłębić tajniki algorytmiki powinna zaznajomić się z drzewem BST, ponieważ jest to jedna z podstawowych struktur danych. Na początek kilka podstawowych pojęć. Każdy element w drzewie będziemy nazywać węzłem. Każdy węzeł ma przypisaną wartość (klucz), dla wygody przyjmiemy, że będą to liczby całkowite dodatnie. Oprócz klucza, każdy węzeł posiada dwóch synów (lewego i prawego) i ojca, którzy również są węzłami. Nie możemy jednak przechowywać wartości w węzłach w dowolnym porządku. Aby drzewo nazwać drzewem przeszukiwań binarnych, potrzebne jest nam jeszcze jedno założenie. Otóż wartość każdego węzła ma być przechowywana tak, aby spełniona była własność drzewa BST. Własność drzewa BST mówi, że jeśli weźmiemy dowolny węzeł x, to wartość jego lewego syna jest mniejsza bądź równa wartości węzła x, a wartość jego prawego syna jest większa bądź równa od wartości węzła x.
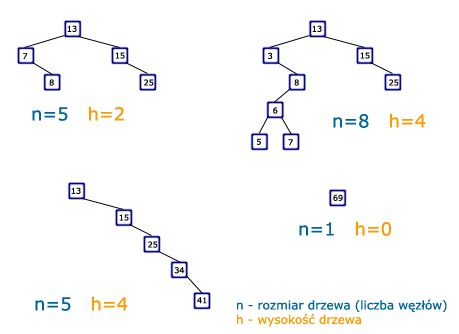
Należy też pamiętać, że niektóre węzły mogą posiadać tylko jednego syna lub wcale ich nie posiadać. Na pewno w każdym drzewie binarnym istnieje jeden taki węzeł, który nie posiada ojca - znajduje się on na górze drzewa i potocznie nazywa się go korzeniem. Dla wygody przyjmuje się, że każdy węzeł posiada ojca i dwóch synów, a jeżeli jakiś węzeł nie ma wartości, to nazywa się go węzłem pustym i oznacza słowem NULL. Przyda się też pojęcie wysokości. Wysokością w drzewie binarnym nazywamy liczbę krawędzi w najdłuższej ścieżce, której początkiem jest korzeń. Poniżej podaję kilka przykładów drzew przeszukiwań binarnych, żebyś mógł szybciej oswoić się z nową strukturą.
Proste zadankaZanim przejdziesz do dalszej części lektury, w ramach ćwiczeń proponuję, abyś wykonał kilka prostych zadań:
(4 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com