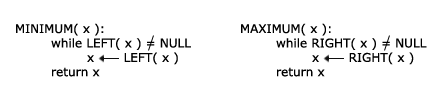Drzewa przeszukiwań binarnych
14.12.2009 - Michał Karpiński
 Maksimum i minimumWiedząc jak wyszukać element w drzewie BST nietrudno będzie skonstruować metody do znajdowania elementu o wartości najmniejszej lub największej. Aby znaleźć element najmniejszy wystarczy przeszukiwać drzewo „w lewo” dopóki nie napotkamy na węzeł pusty. Poprawność tego algorytmu wynika wprost z własności drzewa BST: wszak lewy syn ma zawsze mniejszą wartość od sprawdzanego węzła.
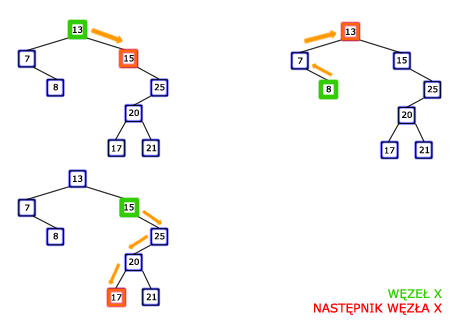
Oczywistym jest, że w przypadku znajdowania maksimum drzewo BST przeszukujemy „w prawo”. Podobnie jak w przypadku wyszukiwania elementu o podanej wartości, procedury MINIMUM i MAXIMUM przechodzą po ścieżce w dół drzewa, czyli obie procedury wykonają się w czasie O(h), gdzie h jest wysokością drzewa. Poprzednik i następnikW tym rozdziale spróbujemy rozwiązać następujące zadanie: dla danego węzła x znaleźć jego następnik tzn. węzeł, który byłby wypisany jako następny po x-ie używając metody inorder. Innymi słowy, gdybyśmy utworzyli uporządkowaną listę wszystkich wartości węzłów to następnik węzła o indeksie i miałby indeks i+1. Oczywiście jeśli x jest węzłem o maksymalnej wartości, to jego następnik jest węzłem pustym. Oto kilka przykładów drzew, w których pokazani są następnicy pewnych wybranych węzłów.
Algorytm będzie rozpatrywał dwa przypadki: jeśli prawy syn węzła x jest niepusty, to następnikiem jest minimum poddrzewa o korzeniu będącym prawym synem węzła x. W przeciwnym wypadku następnikiem jest najniższy przodek węzła x, którego lewy syn jest także przodkiem x.
Druga część algorytmu na pierwszy rzut oka może wydawać się skomplikowana, ale wystarczy kilka razy wykonać tą operację na przykładowych drzewach, żeby procedura SUCCESSOR stała się jaśniejsza. Czas działania procedury wyszukania następnika działa w czasie O(h) (gdzie h jest wysokością drzewa), ponieważ przechodzimy drzewo po ścieżce w dół, albo w górę. Ćwiczenia
(4 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com