Drzewa przeszukiwań binarnych
14.12.2009 - Michał Karpiński
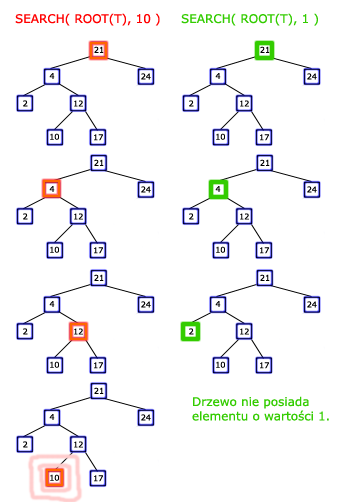
 Wyszukiwanie elementuBST nie nazywało by się drzewem przeszukiwań, gdyby nie można było w nim wyszukiwać elementów. W tym rozdziale pokażę algorytm, który sprawdzi, czy element o podanej wartości znajduje się w drzewie BST.
Powyższe definicje są równoważne (wykonują to samo zadanie), z tym jednak zastrzeżeniem, że definicja po lewej jest bardziej intuicyjna, natomiast prawą definicję lepiej jest stosować w praktyce, bo na większości komputerów wykona się szybciej. W celach edukacyjnych będziemy się zajmowali procedurą rekurencyjną. Zrozumienie instrukcji w niej zawartych nie jest trudne. Jeżeli chcemy sprawdzić czy w drzewie BST ( zaczynając od węzła x) jest klucz k, to jeśli wartość x jest równa k ( k = KEY(x) ), to zwracamy x. Węzeł x zostanie również zwrócony w wypadku, gdy jest węzłem pustym. W przeciwnym wypadku dalej przeszukujemy drzewo w zależności od tego, czy szukana wartość jest mniejsza od aktualnej, czy większa. Ten krok wynika wprost z własności drzewa BST. Procedurę wyszukiwania rozpoczynamy oczywiście w korzeniu i z każdym krokiem schodzimy po ścieżce w dół dopóki nie natkniemy się na szukany węzeł lub nie znajdziemy się w węźle pustym. Oto przykłady działania procedury SEARCH(x, k):
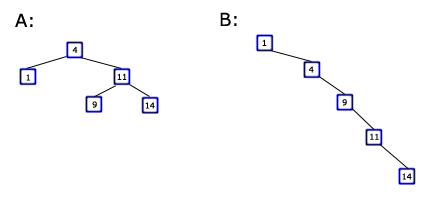
Zastanówmy się teraz jak długo zajmie wyszukanie elementu w drzewie BST. Przyjrzyjmy się poniższym drzewom. Widać, że złożone są z tego samego zbioru kluczy, lecz mimo to, znacznie różnią się od siebie.
Rozważmy przypadek pesymistyczny - chcemy wyszukać element o wartości 14. W przypadku drzewa A musimy wywołać funkcję rekurencyjną tylko dwa razy, natomiast przeszukując drzewo B takich wywołań będzie cztery. Wniosek z powyższej obserwacji jest następujący: czas działania procedury SEARCH, wynosi O(h), gdzie h jest wysokością drzewa. Kilka zadań kontrolnych
(4 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com