Drzewa przeszukiwań binarnych
14.12.2009 - Michał Karpiński
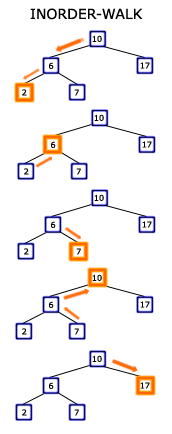
 Przechodzenie drzewaRozważmy następujące zadanie: chcemy wypisać wszystkie wartości węzłów w drzewie przeszukiwań binarnych w sposób uporządkowany, a jedyne co mamy dane, to wskaźnik do korzenia drzewa. Najprostszym sposobem wykonania tego zadania jest użycie algorytmu rekurencyjnego zwanego przechodzeniem drzewa metodą inorder. Zastanówmy się, jak taki algorytm mógłby wyglądać. Na początku mamy korzeń. Wiemy, że spełnia on własność drzewa BST, czyli jego lewy syn ma większą wartość od wartości korzenia, a wartość korzenia jest mniejsza od wartości prawego syna. Dlatego w takiej kolejności należy wyświetlić wartości tych trzech węzłów: lewy syn, korzeń, prawy syn. Dla małego drzewa (o rozmiarze 3 i wysokości 1) zadanie jest rozwiązane, ale my chcemy wyświetlić wartości dowolnych drzew. Wystarczy zauważyć, że lewy syn i prawy syn korzenia również są drzewami BST. Jedyne co wystarczy zrobić to powtórzyć powyższy krok rekurencyjny.
Podana definicja mówi, że gdy odpalimy procedurę INORDER-WALK na węźle x, to jeśli x nie jest węzłem pustym to powtórzmy procedurę dla jego lewego syna ( LEFT( x ) ), wyświetlmy wartość węzła x ( KEY( x ) ) i powtórzmy procedurę dla prawego syna ( RIGHT( x ) ). Żeby wyświetlić wszystkie wartości drzewa BST wystarczy wywołać metodę inorder na korzeniu drzewa: INORDER-WALK( ROOT( T ) ) Można też przechodzić drzewo innymi sposobami. Wypisanie klucza korzenia po wypisaniu wartości znajdujących się w obu poddrzewach nazywa się metodą postorder. Natomiast wypisanie wartości korzenia przed wypisaniem wartości jego synów nosi nazwę metody preorder. W ramach ćwiczeń zastanów się jak powinny wyglądać definicje obu tych metod. Możesz skorzystać z definicji procedury INORDER-WALK i pozamieniać miejscami odpowiednie instrukcje w celu stworzenia procedur POSTORDER-WALK i PREORDER-WALK. Czas działania procedur przechodzenia drzewa BST jest wprost proporcjonalny do rozmiaru drzewa. Dla przykładu weźmy procedurę INORDER-WALK. Z definicji tej procedury widać, że każdy węzeł zostanie odwiedzony dokładnie raz. W takiej sytuacji mówimy, że algorytm działa w czasie O(n). Więcej o notacji O znajdziesz tutaj. (4 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com