Drzewce
03.10.2010 - Michał Karpiński
   Procedura "Split" i "Merge"Omówiliśmy już najważniejsze algorytmy operowania na drzewcach. W zupełności wystarczy nam to do rozwiązywania prostych problemów, jednak czasami zachodzi potrzeba pójścia o jeden krok dalej. Załóżmy, że liczba drzewców, którymi będziemy operowali jest istotnie większa niż jeden. Oczywistym jest fakt, że potrzebujemy dodatkowych procedur, żeby w pełni móc zarządzać wszystkimi drzewcami. Operacje, którymi będziemy zajmowali się w tym rozdziale to: rozdzielanie (split) drzewca na dwa osobne drzewce oraz scalanie (merge) dwóch różnych drzewców w jeden. Najpierw weźmiemy pod lupę prostszą z tych metod, czyli SplitZadanie brzmi następująco: dla danego drzewca Procedura rozdzielania jest prosta, ponieważ stoi za nią prosty trik. Aby podzielić drzewiec na dwie części zgodnie z naszymi założeniami wystarczy wstawić do drzewca T element o kluczu k i maksymalnym priorytecie - większym niż wszystkie inne w drzewcu (element ten nazwijmy Zobaczmy co się stanie: najpierw - według algorytmu wstawiania - Przyjrzyjmy się teraz synom korzenia 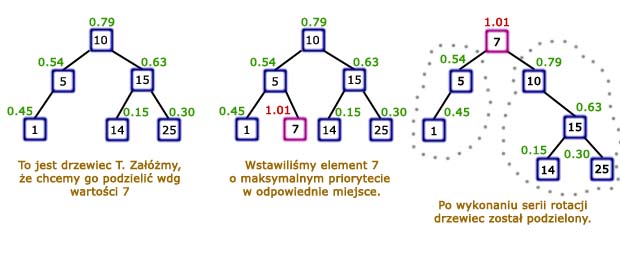
Najlepsze w tej metodzie, to czas jego działania. Żeby podzielić drzewiec wystarczy wstawić do niego jeden element, czyli czas podziału jest równy czasowi jednokrotnego wykonania procedury MergePrzy scalaniu dwóch drzewców nie zawsze możemy zastosować powyższy trik. W praktyce bardzo rzadko zdarza się taka sytuacja, bo aby scalić drzewce Można wtedy odwrócić proces podziału w następujący sposób: wiedząc, że największy element Teraz wystarczy usunąć z drzewca element 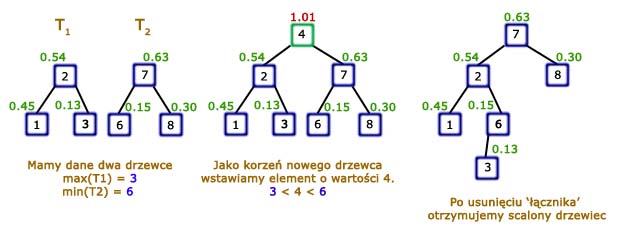
Czas wykonania powyższej metody jest równy czasowi jednokrotnego wywołania procedury Jak już wspomnieliśmy: nieczęsto zdarzają się tak sprzyjające warunki, jak w naszym przykładzie. Dla ogólnych przypadków trzeba się trochę bardziej namęczyć. Jednym ze sposobów połączenia drzewców (2 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


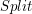 .
. i wartości
i wartości  , podziel
, podziel 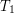 i
i 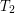 , gdzie w
, gdzie w 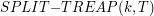 .
. ). Np. jeśli założyliśmy, że wartości priorytetów są z przedziału od 0 do 1, to dla
). Np. jeśli założyliśmy, że wartości priorytetów są z przedziału od 0 do 1, to dla 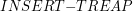 .
. w
w ![$ \langle key[x],key[y] \rangle $](/files/tex/d6f7112bcbb8e1da62641a8bafef153cb1e80064.png) i nowemu elementowi
i nowemu elementowi  przypisujemy pola:
przypisujemy pola: ![$ key[z]=k $](/files/tex/c8ce9d31ea3d406120b09c480980faaeec2303b9.png) ,
, ![$ left[z]=root[T_1] $](/files/tex/b48891f65a0f878de3108636a8d4ed7054bb1cc0.png) ,
, ![$ right[z]=root[T_2] $](/files/tex/a340cae8e07c3709e691716bc5d679863c1131d3.png) ,
, ![$ priority[z]=1.01 $](/files/tex/6a25303c9f82af0218662902fa636b0ec0411525.png) (największy możliwy priorytet).
(największy możliwy priorytet).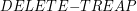 . Były dwa drzewce, zrobił się jeden. Zobaczmy cały ten proces na przykładzie:
. Były dwa drzewce, zrobił się jeden. Zobaczmy cały ten proces na przykładzie: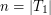 jest mała. Należy wtedy
jest mała. Należy wtedy  razy wykonać procedurę
razy wykonać procedurę 

