Drzewce
03.10.2010 - Michał Karpiński
   Rotacje na drzewie binarnymRatocję w najprostszy sposób można opisać jako zamianę węzła 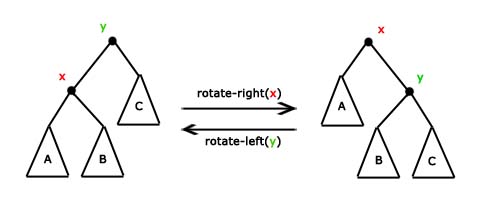
Gdybyśmy przeczytali od lewej do prawej etykiety wszystkich wierzchołków i ich poddrzew przedstawionych na rysunku przed i po wykonaniu rotacji, to powstałby następujący ciąg: Uwaga: niezwykle ważne przy implementacji procedury Wróćmy do przykładu z poprzedniej strony i zastosujmy rotacje do przywrócenia własności kopca po wstawieniu elementu do drzewa: Po dojściu do korzenia kończymy algorytm wstawiania. Klucze zachowały porządek inorder i priorytety zachowały własność kopca. Warto zauważyć, że nie zawsze dochodzimy z nowym elementem aż do korzenia. Sprawdź ile rotacji należało by wykonać w naszym przykładzie, gdyby nowy węzeł miał inny priorytet, np. 0.60. A co jeśli wynosił by 0.10? Gotowa procedura „Insert”Poniżej zapisany jest algorytm wstawiania nowego elementu do drzewca w postaci pseudokodu: 
Procedura (2 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


 z jego ojcem
z jego ojcem  oraz przekierowaniu kilku wskaźników zgodnie z poniższym rysunkiem:
oraz przekierowaniu kilku wskaźników zgodnie z poniższym rysunkiem: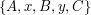 . Prowadzi to do prostego i bardzo ważnego wniosku, że „rotacja zachowuje porządek inorder” i właśnie o to nam chodziło.
. Prowadzi to do prostego i bardzo ważnego wniosku, że „rotacja zachowuje porządek inorder” i właśnie o to nam chodziło.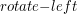 i
i 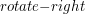 jest pamiętanie o wszystkich wskaźnikach, które są wykorzystywane przy rotacji. Nie tylko przekierowujemy synów
jest pamiętanie o wszystkich wskaźnikach, które są wykorzystywane przy rotacji. Nie tylko przekierowujemy synów 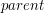 i na to należy zwrócić szczególną uwagę. Nie zapomnijmy też, że podczas rotacji korzeń drzewa może ulec zmianie!
i na to należy zwrócić szczególną uwagę. Nie zapomnijmy też, że podczas rotacji korzeń drzewa może ulec zmianie!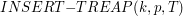 wstawia nowy element o kluczu
wstawia nowy element o kluczu  i priorytecie
i priorytecie  do drzewca
do drzewca  .
.

