Answer these queries

23.02.2010 - Tomasz Górzny
TrudnośćTrudnośćTrudnośćTrudność

W tym artykule prezentuję rozwiązania trzech zadań ze SPOJa. Wszystkie pochodzą z (dość długiego) cyklu "Answer these queries" i (mimo dość podobnie wyglądających sformułowań) wymagają połączenia kilku różnych, i to dość nietrywialnych, pomysłów. Ze względu na zróżnicowany poziom trudności lekturę polecam zarówno początkującym, jak i starym wyjadaczom.

Na wstępie pewnie warto powiedzieć, jakimi zadaniami będziemy się zajmować. Oto one:

  1. GSS1,
  2. GSS3,
  3. GSS2.
Wszystkie polegają na przetwarzaniu zapytań dotyczących ciągu liczb. Ogólny schemat jest taki: dany jest ciąg N liczb całkowitych $ A[1] \ldots A[N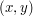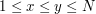] $ oraz zapytania postaci $ (x,y) $, $ 1 \le x \le y \le N $. Odpowiedzią na zapytanie powinna być wartość najlepszego podciągu ciągu $ A[x] \ldots A[y] $, gdzie najlepszy to taki, który ma największą wartość. Bardziej formalnie: $ max \{ val(A[i] \ldots A[j]) | x \le i \le j \le y \} $

To, jak liczymy wartość podciągu $ val(A[i] \ldots A[j]) $, zależy od zadania. W przypadku GSS1 i GSS3 jest to po prostu suma elementów, a w GSS2 suma różnych elementów. Aby urozmaicić (tudzież utrudnić) nam życie, w GSS3 oprócz zapytań pojawiają się także żądania modyfikacji wejściowego ciągu A.

No dobrze, skoro znamy już problem, możemy zaczynać!

Poniżej znajduje się formularz do wysyłania rozwiązań zadań, których sformułowania pojawią się w dalszej części artykułu.
Nie możesz wysyłać i oglądać rowiązań tego zadania ponieważ nie jesteś zalogowany. Zaloguj się lub załóż konto.
5
Twoja ocena: Brak Ocena: 5 (2 ocen)

Copyright © 2008-2010 Wrocławski Portal Informatyczny

design: rafalpolito.com