Struktura problemu
Pomyślmy o strukturze problemu. Podzielmy ciąg ![$ A[a] \ldots A[b] $](/files/tex/99af1e190629594fe83e24c2a793f0803e6a4176.png) na dwie
części:
na dwie
części: ![$ A[a] \ldots A[c] $](/files/tex/a90ef9d9cdb2d809cbcd50403bddb3a5e2de48cb.png) i
i ![$ A[c+1] \ldots A[b] $](/files/tex/79eb5b6e176bade9d815a16f55f7379902b67ccc.png) . Mamy dwa przypadki:
. Mamy dwa przypadki:
- maksymalny podciąg przechodzi przez punkt podziału - wtedy wystarczy wziąć
maksimum z tablicy S odpowiadającej prawej części i minimum z odpowiadającej
lewej części.
- maksymalny podciąg zawiera się w całości w którymś z
![$ A[a] \ldots A[c] $](/files/tex/829b66ca5d0859b5c6cf68954cdb59d29651cf74.png) ,
,
![$ A[c+1] \ldots A[b] $](/files/tex/79eb5b6e176bade9d815a16f55f7379902b67ccc.png) - szukamy wtedy rekurencyjnie.
- szukamy wtedy rekurencyjnie.
Zauważmy, że często liczymy dla pewnych przedziałów minimum, maksimum i
najlepszy możliwy wynik. Użyjmy więc drzewa przedziałowego, aby je spamiętać!
Minimum i maksimum zapamiętamy łatwo, wynik również:
wynik = max( lewy wynik, prawy wynik, prawy max - lewy min)
Teraz używamy tylko ogólnego schematu dla drzew i otrzymujemy czas odpowiedzi
na zapytanie
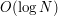
, który nas w pełni satysfakcjonuje. Na koniec rysunek
przedstawiający takie drzewo:
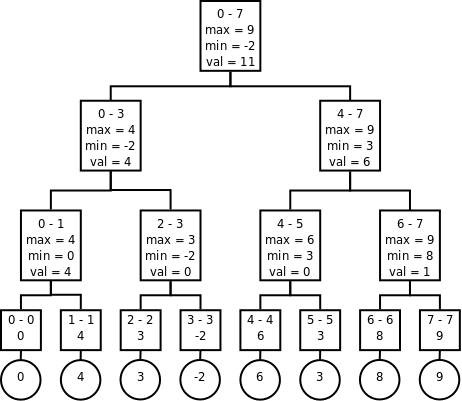
Wygląda na to, że zadanie pierwsze zostało właśnie rozwiązane. Super :)
Praca domowa
Jeżeli sam nie zrobisz, to się nie nauczysz. Serio!
- Zaimplementuj liczenie sum prefiksowych i odpowiadanie na zapytania o sumy
przedziału. Opis zadania:
Wejście:
Pierwsza linia wejścia zawiera liczbę N (1 <= N <= 10^6) - liczbę elemetnów ciągu A.
Druga linia zawiera N liczb - ciąg A ( -10^6 <= A[i] <= 10^6).
Trzecia linia zawiera Q (1 <= Q <= 2*10^6) - liczbę zapytań.
Kolejnych Q linii zawiera pary liczb a i b (1 <= a <= b <= N).
Wyjście:
Dla każdej pary liczb a i b wypisz sumę A[a]+..A[b].
Przykład:
Wejście:
4
1 -2 4 -8
3
2 4
3 3
1 3
Wyjście:
-6
4
3
Swoje rozwiązanie możesz wysłać używając formularza na dole strony.
- Napisz w pseudokodzie (tzn. w pythonie), jak dokładnie powinno wyglądać w drzewie
przedziałowym odpowiadanie na zapytanie o maksimum z przedziału (x,y).

|
Aby sprawdzić poprawność zmień nieco swój kod, tak jak w przykładzie.
|
|
|
- Zaimplementuj zadanie GSS1 :)
Wejście:
Pierwsza linia wejścia zawiera liczbę N (1 <= N <= 125000) - liczbę elemetnów ciągu A.
Druga linia zawiera N liczb - ciąg A ( -10^5 <= A[i] <= 10^5).
Trzecia linia zawiera Q (1 <= Q <= 5*10^5) - liczbę zapytań.
Kolejnych Q linii zawiera pary liczb a i b (1 <= a <= b <= N).
Wyjście:
Dla każdej pary liczb a i b wypisz maksimum z A[x]+..A[y], gdzie a <= x <= y <= b.
Przykład:
Wejście:
4
2 -1 4 -8
3
2 4
1 1
1 3
Wyjście:
4
2
5
Swoje rozwiązanie możesz wysłać już teraz!
- Dla bardziej ambitnych - w tym zadaniu można osiągnąć stały czas odpowiedzi
na zapytania, kosztem większego czasu przetwarzania wstępnego i większego
zużycia pamięci. Jak to zrobić?
Wskazówki techniczne
- W C++ ze względów wydajnościowych polecam użycie do wczytywania/wypisywania printf i scanf zamiast cin i cout. Jeżeli zechcesz wypisać typ long long, obsługuje się go przez "%lld".
- Mała nieścisłość notacyjna - w zapisie
![$ max \{ val(A[i] \ldots A[j]) | x \le i \le j \le y \} $](/files/tex/ecb8fd99ce0df8d4af26d118cdf24d234d88af0d.png) maksimum przebiega również po pustym podciągu (czyli jest zawsze nieujemne).
maksimum przebiega również po pustym podciągu (czyli jest zawsze nieujemne).
- Zadania z pseudokodem są uruchamiane w Pythonie. Należy zadbać o poprawność i spójność wcięć (najlepiej 2 spacje).
Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany.
Zaloguj się lub
załóż konto.




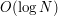 , który nas w pełni satysfakcjonuje. Na koniec rysunek
przedstawiający takie drzewo:
, który nas w pełni satysfakcjonuje. Na koniec rysunek
przedstawiający takie drzewo:



![$ A[a] \ldots A[b] $](/files/tex/99af1e190629594fe83e24c2a793f0803e6a4176.png) na dwie
części:
na dwie
części: ![$ A[a] \ldots A[c] $](/files/tex/a90ef9d9cdb2d809cbcd50403bddb3a5e2de48cb.png) i
i ![$ A[c+1] \ldots A[b] $](/files/tex/79eb5b6e176bade9d815a16f55f7379902b67ccc.png) . Mamy dwa przypadki:
. Mamy dwa przypadki:
![$ A[a] \ldots A[c] $](/files/tex/829b66ca5d0859b5c6cf68954cdb59d29651cf74.png) ,
,
![$ max \{ val(A[i] \ldots A[j]) | x \le i \le j \le y \} $](/files/tex/ecb8fd99ce0df8d4af26d118cdf24d234d88af0d.png) maksimum przebiega również po pustym podciągu (czyli jest zawsze nieujemne).
maksimum przebiega również po pustym podciągu (czyli jest zawsze nieujemne).


