Answer these queries
23.02.2010 - Tomasz Górzny
    Implementacja drzew binarnychNa koniec wypada powiedzieć jeszcze kilka słów o implementacji drzew. Można w każdym węźle trzymać wskaźniki na jego potomków, ale to nie jest najlepsze rozwiązanie. Lepiej zamiast tego przechowywać je w tablicy wg tego schematu: 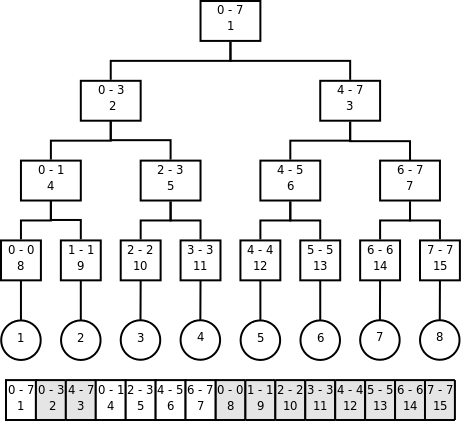
Pozwala to zaoszczędzić nieco pamięci na wskaźnikach, trochę przyspiesza obliczenia i pozwala zapisywać rzeczy w bardziej elegancki (choć być może mniej czytelny) sposób - na przykład budować drzewa od dołu w górę. Powiedzmy, że chcielibyśmy w drzewie przechowywać sumę przedziału. Kod wyglądałby tak:
Praca domowa
Na dokładkęJeżeli jeszcze czujesz niedosyt, polecam zrobienie zadania GSS6 na SPOJu. Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany. Zaloguj się lub załóż konto.
(4 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com




