Answer these queries
23.02.2010 - Tomasz Górzny
    GSS3Dla porządku i czytelności:
Wstępne rozważaniaZadanie polega na odpowiedzi na takie same zapytania, jak w poprzednim, z jedną drobną różnicą: mogą pojawiać się żądania modyfikacji wejściowego ciągu. Tylko.. czy aby na pewno jest to drobna różnica? Zacznijmy od skopiowania struktury z pierwszego zadania i zastanówmy się, jak poradzić sobie ze zmianami. Podejście naiwneZmiana wartości jednego elementu powoduje konieczność zmiany wielu sum prefiksowych w naszej strukturze. A dokładniej, jeżeli wartość A[i] zmieni się o x, to do![$ S[i] \ldots S[N] $](/files/tex/03d399c9e0b7be065bb7d11e5cabc287e359c444.png) należy dodać wartość x. Spójrzmy jak wygląda to
w przełożeniu na węzły drzewa (cały czas zakładając, że jesteśmy naiwni): należy dodać wartość x. Spójrzmy jak wygląda to
w przełożeniu na węzły drzewa (cały czas zakładając, że jesteśmy naiwni):
Leniwość obliczeńZauważmy, że w przypadku c) potrafimy dokładnie powiedzieć, jakie będą te wartości po przeliczeniu - minimum i maksimum zmienią się o x, a maksymalny wynik się nie zmieni. Nie ma zatem potrzeby odwiedzania poddrzew. Zachowajmy się zatem leniwie i tego nie róbmy! Czy mimo tego będziemy potrafili odtworzyć wartości, które powinny być w nich zapisane? Tak! Bardziej bym się jednak skłaniał do tego, aby dodać nową wartość do węzła, w której zapiszemy o ile powinniśmy zmodyfikować poddrzewa. Oczywiście później w trakcie ich odwiedzania dokonujemy tych odpowiednich modyfikacji. Nazwijmy tę nową wartość add. Zobaczmy jak teraz będzie wyglądało drzewo z poprzedniego przykładu: 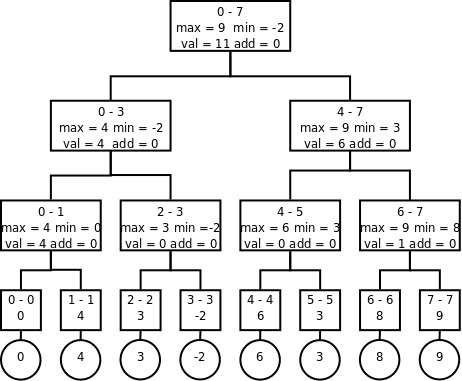
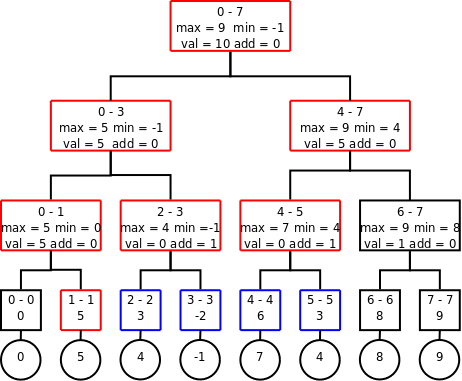
Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany. Zaloguj się lub załóż konto.
(4 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


![$ A[1] \ldots A[N] $](/files/tex/148635fc45adad7af4a65142f7f7af64d00cb001.png) - ciąg wejściowy
- ciąg wejściowy
![$ val(A[i] \ldots A[j]) = A[i] + \ldots + A[j] $](/files/tex/485ec77c4f099e71df3afe08afa896bcb20d364a.png)


