Rozpisujemy operacje na drzewie
Warto zauważyć, że mechanizm odwlekania zastosowany w 2 zadaniu jest tutaj
niewystarczający - pozwala odtworzyć tylko teraźniejsze maksimum, bez tego
na przestrzeni czasu. Jest na to prosta rada - trzeba dodać nowe pole do węzła!
Podsumujmy informacje przechowywane w węźle:
- max - maksimum na przedziale
- hmax - maksimum na przestrzeni czasu na przedziale (hmax = highest max)
- add - wartość dodania dla poddrzew (dla operacji odwlekanych)
- hadd - maksymalna wartość dodania od rozpoczęcia odwlekania w wierzchołku
- lewy, prawy - synowie
- a,b,c - reprezentowany przedział [a,b] i jego podział [a,c], [c+1, b]
Na początek napiszmy obliczanie wartości z poddrzew.
1
2
3
4
5
| oblicz ( v )
// zakładam, że add i hadd są równe zero
// później pokażę, jak to zapewnić
v.max = max( v.lewy.max, v.prawy.max )
v.hmax = max( v.lewy.hmax, v.prawy.hmax ) |
Dodawanie wartości do przedziału
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| dodaj ( v, begin, end, val )
if begin = v.a and end = v.b
v.max = v.max + val
v.hmax = max ( v.hmax, v.max )
v.add = v.add + val
v.hadd = max ( v.hadd, v.add )
return
//zakładam, że add i hadd są równe zero
if end <= v.c
dodaj ( v.lewy, begin, end, val )
else if end >= v.c + 1
dodaj ( v.prawy, begin, end, val )
else
dodaj ( v.lewy, begin, v.c, val )
dodaj ( v.prawy, v.c + 1, end, val )
oblicz ( v ) |
Wykonanie odwleczonych operacji - tym razem nie można po prostu wykonać
dodawania, bo w międzyczasie mogła się pojawić większa wartość i pole z
maksimum na przestrzeni czasu nie byłoby dobrze wyznaczone.
1
2
3
4
5
6
7
8
| przeliczOdwleczone ( v )
v.lewy.hmax = max ( v.lewy.hmax, v.lewy.max + v.hadd )
v.lewy.max = v.lewy.max + v.add
v.lewy.hadd = max ( v.lewy.hadd, v.lewy.add + v.hadd )
v.lewy.add = v.lewy.add + v.add
(analogicznie dla prawego)
v.add = 0
v.hadd = 0 |
Wyjaśnienie linii nr 2 - mogły zaistnieć 2 okoliczności, w których zostało
ustalone maksimum na przestrzeni czasu:
- w czasie przeglądania tego wierzchołka - jest wtedy zapisane w hmax
- pomiędzy poprzednim, a aktualnym odwiedzeniem - były wtedy wykonywane
operacje dodania obejmujące swoim zasięgiem cały przedział, o których wiemy,
że sumowało się do add, a maksimum z tych dodań wynosiło hadd.
Podobna sytuacja jest z hadd.
Czas działania
Każda wykonywana operacja - tzn. odpowiedź na zapytanie i dodanie elementu do
sum sufiksowych jest elementarną operacją na drzewie przedziałowym - stąd jej
czas będzie wynosił
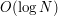
. Stąd całkowity czas działania to
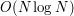
plus
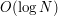
na każde zapytanie.
Praca domowa
- Pola add i hadd są zbędne. Pokaż jak usunąć je z drzewa.

|
Napisz procedurę wylicz_hadd(v), która wyliczy brakującą
wartość hadd. Jeżeli wyznaczenie wartości jest niemożliwe, to zwróć:
- -1 gdy hadd może przyjąć wiele wartości, ale nie wpłynie to na pozostałe zmienne
- -2 w przypadku, gdy nie da się odtworzyć wcześniejszej sytuacji
|
|
|
- Pokaż jak sobie radzić bez zerowania wspomnianych pól.
- Zapisz procedurę przeliczOdwleczone za pomocą dodań do poddrzew.
- Zaimplementuj zadanie GSS2. :) Opis zadania:
Wejście:
Pierwsza linia wejścia zawiera liczbę N (1 <= N <= 125000) - liczbę elemetnów ciągu A.
Druga linia zawiera N liczb - ciąg A ( -10^5 <= A[i] <= 10^5).
Trzecia linia zawiera Q (1 <= Q <= 5*10^5) - liczbę zapytań.
Kolejnych Q linii zawiera pary liczb a i b (1 <= a <= b <= N).
Wyjście:
Dla każdej pary liczb a i b wypisz maksimum z sum różnych elementów ciągu A[x]+..A[y], gdzie a <= x <= y <= b.
Przykład:
Wejście:
5
4 -2 -2 3 -1
3
1 5
1 1
2 3
Wyjście:
5
4
0
- Wyzwanie - rozwiąż na SPOJu zadanie GSS2 używając mniej niż 2 MB pamięci. (link)
Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany.
Zaloguj się lub
załóż konto.




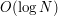 . Stąd całkowity czas działania to
. Stąd całkowity czas działania to 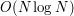 plus
plus 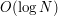 na każde zapytanie.
na każde zapytanie.




