Kto jest najbogatszy i czy to naprawdę miłość?
25.02.2010 - Agata Murawska
  Czy zdarzyło Wam się kiedyś zakochać? Strasznie głupia sprawa, ale Alicja i Bob nie są pewni, co do siebie czują. Żadne z nich nie zdecyduje się powiedzieć drugiemu, że go (nie) kocha, póki nie usłyszy podobnej deklaracji od drugiej strony.
Sytuacja wydaje się bez wyjścia - póki któreś z nich nie "pęknie", będą trwali w zawieszeniu. Zawieszona Alicja nie jest w stanie programować, a Bob projektować protokołów kryptograficznych - trzeba więc coś zrobić, żeby pomóc nieszczęsnej parze. Wystarczy, że będą wiedzieli, czy to miłość - i znów będą w stanie normalnie funkcjonować.

Anton i Bill są multimiliarderami. Nie chwalą się swoimi majątkami publicznie, bo jeszcze okazałoby się, że muszą zapłacić jakiś podatek - są jednak ciekawi, który z nich jest bogatszy. Żaden nie zamierza podawać drugiemu swojego stanu konta, a mimo to są zdeterminowani rozstrzygnąć ten spór o wielką kasę.
Jak sugeruje nazwa, problem obliczeń wielopodmiotowych ma następującą postać:

Oczywiście, obliczenia te będą bezpieczne także, jeśli znajdziemy bezstronną, zaufaną osobę trzecią, której możemy powierzyć najskrytsze sekrety. Wtedy po prostu obaj uczestnicy przesyłają swoje dane wejściowe zaufanej stronie, która dokonuje obliczeń i rozdziela wyniki. Nie ma w tym żadnej magii, poza tą jedynie, że niestety, o aż tak zaufane osoby jest dziś ciężko. Zwłaszcza, jeśli jest się multimiliarderem. Porzućmy zatem marzenia o innym, piękniejszym świecie (Po co nam w takim świecie kryptografia? Przecież tam każdemu możemy ufać!) i wróćmy na ziemię. Jak zatem rozwiązać problem Alicji i Boba nie mając nikogo zaufanego na podorędziu, a jedynie parę być-może-zakochanych? Załóżmy na początek, że Alicja i Bob są wobec siebie uczciwi i nie będą próbowali się okłamywać.
(1 ocena) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com



 oznacza odpowiedź na pytanie, czy Alicja kocha Boba, zaś
oznacza odpowiedź na pytanie, czy Alicja kocha Boba, zaś  pozwala stwierdzić, czy Bob kocha Alicję. Wówczas
pozwala stwierdzić, czy Bob kocha Alicję. Wówczas 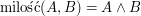 - czyli miłość jest wtedy, kiedy Alicja kocha Boba i Bob kocha Alicję.
- czyli miłość jest wtedy, kiedy Alicja kocha Boba i Bob kocha Alicję.
 osób:
osób: 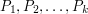 , z których każda ma dostęp do jednego fragmentu informacji, odpowiednio
, z których każda ma dostęp do jednego fragmentu informacji, odpowiednio 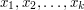 . Osoby te stają wspólnie przed zadaniem obliczenia funkcji
. Osoby te stają wspólnie przed zadaniem obliczenia funkcji 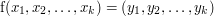 . Założenia przyjmowane w tym modelu są następujące:
. Założenia przyjmowane w tym modelu są następujące: 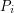 ma dostęp do informacji
ma dostęp do informacji 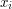
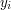 funkcji
funkcji