Kto jest najbogatszy i czy to naprawdę miłość?
25.02.2010 - Agata Murawska
  Na początek - coś dziwnego
Zaczniemy od skonstruowania funkcji transferu utajnionego. Cóż to takiego?
Oznaczenia:
1.
Alicja losuje dwie liczby, 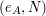 - klucz publiczny Alicji (z protokołu RSA) - klucz publiczny Alicji (z protokołu RSA)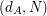 - klucz prywatny Alicji (j.w.) - klucz prywatny Alicji (j.w.)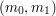 - argument Alicji - argument Alicji - argument Boba ( - argument Boba (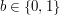 ) )
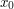 i i 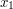 . .2. Alicja przekazuje Bobowi swój klucz publiczny 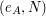 oraz wylosowaną parę oraz wylosowaną parę 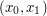 . .3. Bob losuje liczbę  i wybiera i wybiera  - numer wiadomości, którą chce otrzymać. - numer wiadomości, którą chce otrzymać.4. Bob szyfruje  przy pomocy klucza publicznego Alicji, a następnie dodaje do niego przy pomocy klucza publicznego Alicji, a następnie dodaje do niego 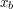 - -  -tą liczbę przekazaną mu przez Alicję. Sumę przekształca dalej -tą liczbę przekazaną mu przez Alicję. Sumę przekształca dalej 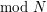 . .5. Otrzymane 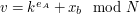 Bob przesyła do Alicji. Bob przesyła do Alicji.6. Alicja oblicza 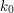 jako wynik odszyfrowania jako wynik odszyfrowania 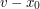 oraz oraz 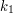 jako odszyfrowane jako odszyfrowane 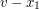 . Zauważmy w tym miejscu, że . Zauważmy w tym miejscu, że 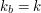 , druga z wartości nas nie interesuje. , druga z wartości nas nie interesuje.7. Ponieważ Alicja nie wie, o którą wartość mogło chodzić Bobowi, odsyła do niego parę 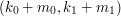 8. Bob, odejmując od interesującego go elementu pary 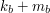 znaną sobie liczbę znaną sobie liczbę  , otrzymuje , otrzymuje  -ty element pary. -ty element pary.
Spróbuj uogólnić powyższą procedurę na protokół transferu utajnionego dla wyboru jednej z  wartości. wartości.
..ale co z tą miłością?!
Wszystko to bardzo pięknie, ale jak to się ma do problemu potencjalnej miłości Boba i Alicji? Myli się, kto sądzi, że nijak. Używając transferu utajnionego możemy rozwiązać problem zakochanych niemal od ręki!
Zauważmy, że jeśli Alicja kocha Boba, to po wykonaniu tego protokołu, wie, czy jej uczucie jest odwzajemnione. Podobnie jest, jeśli Bob kocha Alicję.
Przypomnijmy, że 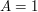 jeśli Alicja kocha Boba i jeśli Alicja kocha Boba i 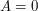 w przeciwnym razie, podobnie dla wartości w przeciwnym razie, podobnie dla wartości  .Teraz wystarczy, że argumentem Alicji będzie para .Teraz wystarczy, że argumentem Alicji będzie para 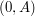 , zaś argumentem Boba (czyli liczbą, o którą pyta Bob) będzie , zaś argumentem Boba (czyli liczbą, o którą pyta Bob) będzie  . Bob po otrzymaniu wyniku przesyła go jeszcze do Alicji. . Bob po otrzymaniu wyniku przesyła go jeszcze do Alicji.Dlaczego to działa? No cóż, jeśli 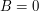 to Bob otrzyma to Bob otrzyma  niezależnie od tego, co sądzi o nim jego dziewczyna. Jeśli zaś niezależnie od tego, co sądzi o nim jego dziewczyna. Jeśli zaś 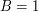 , to Bob w wyniku dostanie odpowiedź Alicji, gdyż to jej głos jest w tym wypadku decydujący. Kryzys zażegnany! , to Bob w wyniku dostanie odpowiedź Alicji, gdyż to jej głos jest w tym wypadku decydujący. Kryzys zażegnany!
No, może nie do końca. Na początku powiedzieliśmy, że zakładamy o obu uczestnikach, że są uczciwi. A przecież jeśli Bob nie kocha Alicji, może zdobyć informacje o jej uczuciu w prosty sposób:
Ataki na protokoły kryptograficzne można podzielić na dwie zasadnicze kategorie:
Jeśli Alicja nie kocha Boba, to nie ma pojęcia, o którą wartość on pytał – a w efekcie, czy ją oszukał, czy nie. Wydaje się to trochę nieuczciwe – niekochająca Alicja nie wie, czy jest niekochana, a niekochający Bob potrafi to sprawdzić. Może zatem nie powinniśmy trzymać się ról w protokole? Prosty rzut monetą pozwoli na ustalenie, która ze stron będzie tworzyć parę liczb, a która będzie jedną z tych liczb pobierać. Czy jednak potrafimy uczciwie rzucać monetą?
(1 ocena) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


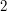 liczby:
liczby: 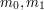 . Bob chce poznać jedną z tych liczb, ale tak, żeby Alicja nie wiedziała, o którą liczbę poprosił. Nie może przy tym poznać drugiej z liczb posiadanych przez Alicję.
. Bob chce poznać jedną z tych liczb, ale tak, żeby Alicja nie wiedziała, o którą liczbę poprosił. Nie może przy tym poznać drugiej z liczb posiadanych przez Alicję.
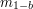 ? Alicja wysyła do niego
? Alicja wysyła do niego 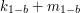 , gdyby zatem Bob mógł obliczyć
, gdyby zatem Bob mógł obliczyć 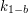 , potrafiłby też znaleźć
, potrafiłby też znaleźć 
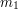 , ale odpowie tak, jakby prosił o
, ale odpowie tak, jakby prosił o 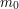 .
Czy Alicja może zorientować się, że Bob ją oszukuje? Tak, ale tylko jeśli go kocha. Czy potrafisz to pokazać?
.
Czy Alicja może zorientować się, że Bob ją oszukuje? Tak, ale tylko jeśli go kocha. Czy potrafisz to pokazać? 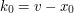 i wie, że
i wie, że 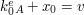 . Oczywiście, wartość nie będzie się zgadzać, bo Bob chciał od Alicji „wyciągnąć” jej odpowiedź, a więc musiał do zaszyfrowanego
. Oczywiście, wartość nie będzie się zgadzać, bo Bob chciał od Alicji „wyciągnąć” jej odpowiedź, a więc musiał do zaszyfrowanego 

