
Wszystkie schematy kryptografii asymetrycznej opierają się na jednym podstawowym założeniu - nasz klucz prywatny musi być dla nas dostępny. Co zatem zrobić, gdy był zapisany na zepsutej karcie magnetycznej, zagubionym gwizdku USB czy po prostu na dysku, który uległ awarii?
Jeśli w przeszłości byliśmy wystarczająco zapobiegliwi i opowiedzieliśmy nasz sekret komuś innemu, jesteśmy uratowani.
Zaraz, zaraz! Ale jak to: opowiedzieliśmy nasz sekret?! Przecież klucze prywatne nie służą do tego, żeby rozpowiadać je komukolwiek!
Racja - dlatego właśnie nauczymy się robić to w sposób bezpieczny. Powierzymy nasz wielki sekret nie jednej osobie, a wielu - ale tak, że każda będzie znać tylko fragment, z którego nie da się wywnioskować nic konkretnego. Sprytne, prawda?
Oczywiście, metody dzielenia sekretu, które omówimy za chwilę, nadają się równie dobrze do przechowywania kopii zapasowej naszego klucza prywatnego, jak i do zabezpieczania sejfu, czy przekazywania kolejnym pokoleniom rodzinnej tajemnicy.
Podzielimy się po równo..
Jak najprościej podzielić sekret? Powiedzmy, że klucz prywatny Alicji, 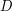 , ma zostać podzielony między
, ma zostać podzielony między  osób tak, żeby żadna z nich nie mogła samodzielnie odtworzyć całej wiadomości. Posłuży się ona w tym celu operacją XOR i losowością.
osób tak, żeby żadna z nich nie mogła samodzielnie odtworzyć całej wiadomości. Posłuży się ona w tym celu operacją XOR i losowością.
XOR, czyli inaczej
alternatywa wykluczająca (eXclusive OR) to operacja na bitach. Jej działanie przedstawia tabelka:
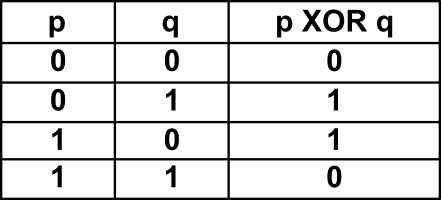
Istotne jest, że przy operacji XOR nie ma znaczenia rozstawienie nawiasów ani kolejność argumentów. Spróbuj udowodnić tę własność!
Diagram Venna dla operacji XOR wygląda tak:

Często stosowane oznaczenia na tę operację to np
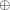
i
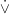
.
XOR można przedstawić jako:
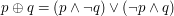
Cały algorytm podziału sekretu jest stosunkowo prosty:
1. Losujemy
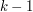
ciągów bitów
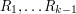
o długości takiej, jak długość
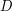
2. Obliczamy
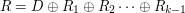
(na każdym bicie wiadomości osobno).
3. Pierwszym
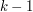
osobom przekazujemy po jednym ciągu bitów
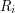
(każdej osobie inny ciąg).
4. Ostatnia osoba otrzymuje szyfr
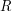
.
Jak Alicja może odzyskać klucz mając wszystkie ciągi 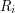 oraz wygenerowany przy ich pomocy i z użyciem
oraz wygenerowany przy ich pomocy i z użyciem 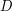 ciąg
ciąg 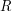 ?
?
Skoro 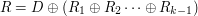 , to można zauważyć, że
, to można zauważyć, że 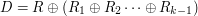 . Jest nam wszystko jedno, w jakiej kolejności będziemy wykonywać obliczenia (XOR jest przemienny), ważne, że mając wiadomości od wszystkich
. Jest nam wszystko jedno, w jakiej kolejności będziemy wykonywać obliczenia (XOR jest przemienny), ważne, że mając wiadomości od wszystkich  osób - potrafimy odtworzyć
osób - potrafimy odtworzyć 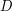 .
.
Równocześnie, ponieważ 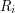 były losowe, znajomość któregokolwiek z nich nic nie daje osobie, której powierzymy jeden z takich ciągów. Podobnie znajomość samego
były losowe, znajomość któregokolwiek z nich nic nie daje osobie, której powierzymy jeden z takich ciągów. Podobnie znajomość samego 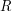 , powstałego przez losowe zgaszanie i zapalanie bitów w oryginalnym podpisie, nie daje żadnej wiedzy o
, powstałego przez losowe zgaszanie i zapalanie bitów w oryginalnym podpisie, nie daje żadnej wiedzy o 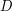 .
.
..a jednak to nie było mądre.
Czy zatem Alicja może spać spokojnie? Nie całkiem.
Żadna ilość osób mniejsza, niż  , nie jest w stanie odtworzyć naszej wiadomości - jeśli wśród tych osób nie ma ostatniej, posiadającej
, nie jest w stanie odtworzyć naszej wiadomości - jeśli wśród tych osób nie ma ostatniej, posiadającej 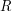 , ta obserwacja jest oczywista, bo generowaliśmy
, ta obserwacja jest oczywista, bo generowaliśmy 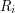 bez związku z naszym kluczem. Ale nawet jeśli
bez związku z naszym kluczem. Ale nawet jeśli 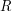 jest znane, a brakuje choćby jednego z
jest znane, a brakuje choćby jednego z 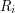 jest dokładnie tak samo źle - każdy bit wiadomości, powstałej przez "xorowanie" posiadanej przez nas części danych, mógł zostać zmieniony tym ostatnim losowym ciągiem (widać to wyraźnie, jeśli popatrzeć uważnie na tabelkę operacji - z wartości
jest dokładnie tak samo źle - każdy bit wiadomości, powstałej przez "xorowanie" posiadanej przez nas części danych, mógł zostać zmieniony tym ostatnim losowym ciągiem (widać to wyraźnie, jeśli popatrzeć uważnie na tabelkę operacji - z wartości  da się zrobić przy pomocy
da się zrobić przy pomocy 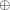 zarówno
zarówno  jak i
jak i  , podobnie z wartości
, podobnie z wartości  )
)
Na pierwszy rzut oka wydaje się, że to dobrze - ale co, jeśli Alicja pokłóci się z jedną z zaufanych osób, przyjaciółka wyjedzie na narty, albo, o zgrozo, ktoś zgubi tajną liczbę, która została mu powierzona? Och, oczywiście my, na miejscu Alicji, mogliśmy po prostu rozsiać informację na jakichś serwerach, zamiast ufać znajomym. Jednak nadal, jeśli jeden z nich uległ awarii, jesteśmy w kropce, zwłaszcza, jeśli ta awaria spowodowała uszkodzenie fragmentu wiadomości. Nie będzie możliwe odzyskanie "sekretu", niezależnie od tego, jak był ważny.
W idealnym świecie nieskończonej pamięci
Powiedzmy, że chcemy podzielić sekret między
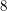
osób, z których każde
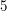
ma móc go odtworzyć. Można wówczas dla każdego pięcioosobowego podzbioru stworzyć osobny podział sekretu w taki sposób, jak powyżej. Ile jest takich podziałów sekretu? A co, jeśli mamy do obdarowania sekretem więcej, na przykład
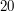
osób, a odtworzyć informację może dowolne
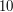
z nich?
A może istnieje lepsza metoda? Taka, w której obrażenie się kilku osób (o ile oczywiście nie będzie ich za dużo) nie spowoduje katastrofy? Na nasze (i Alicji) szczęście - istnieje. Jak zwykle w takich przypadkach, ulepszenie efektu końcowego zwiększa też niestety poziom skomplikowania rozwiązania - chyba, że dysponujemy nieograniczoną pamięcią


 Istotne jest, że przy operacji XOR nie ma znaczenia rozstawienie nawiasów ani kolejność argumentów. Spróbuj udowodnić tę własność!
Istotne jest, że przy operacji XOR nie ma znaczenia rozstawienie nawiasów ani kolejność argumentów. Spróbuj udowodnić tę własność!  Często stosowane oznaczenia na tę operację to np
Często stosowane oznaczenia na tę operację to np 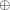 i
i 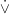 .
XOR można przedstawić jako:
.
XOR można przedstawić jako: 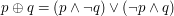
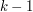 ciągów bitów
ciągów bitów 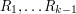 o długości takiej, jak długość
o długości takiej, jak długość 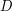
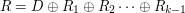 (na każdym bicie wiadomości osobno).
(na każdym bicie wiadomości osobno).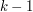 osobom przekazujemy po jednym ciągu bitów
osobom przekazujemy po jednym ciągu bitów 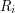 (każdej osobie inny ciąg).
(każdej osobie inny ciąg).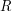 .
.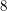 osób, z których każde
osób, z których każde 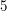 ma móc go odtworzyć. Można wówczas dla każdego pięcioosobowego podzbioru stworzyć osobny podział sekretu w taki sposób, jak powyżej. Ile jest takich podziałów sekretu? A co, jeśli mamy do obdarowania sekretem więcej, na przykład
ma móc go odtworzyć. Można wówczas dla każdego pięcioosobowego podzbioru stworzyć osobny podział sekretu w taki sposób, jak powyżej. Ile jest takich podziałów sekretu? A co, jeśli mamy do obdarowania sekretem więcej, na przykład 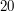 osób, a odtworzyć informację może dowolne
osób, a odtworzyć informację może dowolne 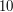 z nich?
z nich?



 osób tak, żeby żadna z nich nie mogła samodzielnie odtworzyć całej wiadomości. Posłuży się ona w tym celu operacją XOR i losowością.
osób tak, żeby żadna z nich nie mogła samodzielnie odtworzyć całej wiadomości. Posłuży się ona w tym celu operacją XOR i losowością.
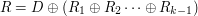 , to można zauważyć, że
, to można zauważyć, że 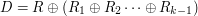 . Jest nam wszystko jedno, w jakiej kolejności będziemy wykonywać obliczenia (XOR jest przemienny), ważne, że mając wiadomości od wszystkich
. Jest nam wszystko jedno, w jakiej kolejności będziemy wykonywać obliczenia (XOR jest przemienny), ważne, że mając wiadomości od wszystkich  da się zrobić przy pomocy
da się zrobić przy pomocy  jak i
jak i 

