Kto jest najbogatszy i czy to naprawdę miłość?
25.02.2010 - Agata Murawska
  Orzeł czy reszka?
Naszej potencjalnie zakochanej parze udało się ustalić, że będą losować, kto będzie tworzyć parę liczb. Jeśli wypadnie reszka, czyli 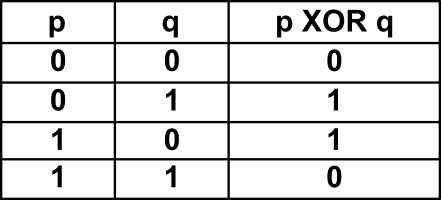 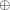 ), można spodziewać się protokołu postaci: ), można spodziewać się protokołu postaci:1. Alicja losuje swój bit, 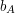 . . 2. Bob losuje swój bit, 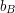 . . 3. Przekazują sobie nawzajem wyniki i obliczają 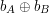 . . Jest tylko jeden problem: jak przekazać wyniki w tym samym momencie, tak, żeby żadne z nich nie mogło oszukać? Nie da się tego niestety w żaden sposób zagwarantować. Rozwiązaniem naszego problemu jest kolejny przykład MPC, tym razem korzystający z protokołu zobowiązania bitowego.
Zobowiązanie bitowe jest protokołem, umożliwiającym uczciwy wybór losowego bitu tak, że strona losująca nie może zmienić losu, a druga strona poznaje los tylko za zgodą losującego.
Zobowiązanie
1. Alicja wybiera bit 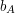 i losuje wiadomość i losuje wiadomość  taką, że jej ostatnim (najmniej znaczącym) bitem jest taką, że jej ostatnim (najmniej znaczącym) bitem jest 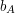 . .2. Alicja szyfruje  za pomocą klucza publicznego za pomocą klucza publicznego 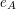 i wysyła Bobowi informację i wysyła Bobowi informację 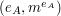 
Odtworzenie bitu
1. Alicja wysyła  do Boba. do Boba.2. Bob wybiera najmniej znaczący bit z  .
Oczywiście, Bob może sprawdzić, czy nie został oszukany - zna klucz .
Oczywiście, Bob może sprawdzić, czy nie został oszukany - zna klucz 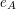 , zatem może zaszyfrować , zatem może zaszyfrować  przy jego pomocy i sprawdzić, czy wynik zgadza się z nadesłanym wcześniej przez Alicję. przy jego pomocy i sprawdzić, czy wynik zgadza się z nadesłanym wcześniej przez Alicję.
Skoro wiemy, jak zobowiązać się do bitu, to potrafimy już także bezpiecznie rzucać monetą. Jak? 1. Alicja losuje 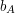 . .2. Bob losuje 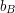 . .3. Alicja zobowiązuje się do 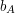 . .4. Bob wysyła 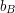 do Alicji. do Alicji.5. Alicja otwiera zobowiązanie dla 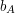 , ujawniając go Bobowi. , ujawniając go Bobowi.6. Każde z nich oblicza 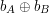 . .Dlaczego ten protokół jest dobry? Bob, wysyłając wylosowany bit 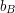 nie wie jeszcze, co wylosowała Alicja - zatem nie może wymusić żadnego wyniku wspólnego losowania. Z kolei Alicja zobowiązała się do nie wie jeszcze, co wylosowała Alicja - zatem nie może wymusić żadnego wyniku wspólnego losowania. Z kolei Alicja zobowiązała się do 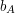 przed poznaniem przed poznaniem 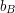 , czyli także bez wiedzy, o wyniku drugiej strony. , czyli także bez wiedzy, o wyniku drugiej strony.Oczywiście, Alicja może odmówić otwarcia zobowiązania - ale jasne jest wtedy, że wynik 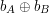 był dla niej niekorzystny. był dla niej niekorzystny.
Najbogatszy człowiek świata
Najbogatszy człowiek świata nie znosi czekać. Na szczęście Anton i Bill nie wiedzą jeszcze, który z nich jest najbogatszy - inaczej moglibyśmy wpaść w poważne tarapaty.
Problem multimiliarderów to przykład podany w pracy, która zapoczątkowała badania nad obliczeniami dwu- i wielopodmiotowymi. Jej autorem jest Andrew Yao, laureat nagrody Turinga z 2000 roku. Przedstawione poniżej rozwiązanie pochodzi właśnie od Yao. Oczywiście, w oryginalnym problemie milionerami byli Alicja i Bob..
Problem bogaczy wydaje się być nieco trudniejszy, niż dwa rozważane przed chwilą. Dla uproszczenia załóżmy, że majątki biznesmenów są z przedziału od  do do 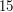 miliardów dolarów - miliardów dolarów - 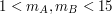 . Ustalmy, że wynikiem działania . Ustalmy, że wynikiem działania 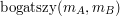 będzie będzie  , jeśli Anton jest bogatszy od Billa ( , jeśli Anton jest bogatszy od Billa (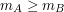 ) i ) i  , w przeciwnym wypadku. , w przeciwnym wypadku.Uwaga: majątki obu bogaczy mogą być wyrażone liczbami  -bitowymi. -bitowymi. Protokół zaproponowany przez Andrew Yao wygląda następująco: 1.
Bill wybiera
2.
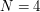 -bitową liczbę -bitową liczbę  . (Dlaczego właśnie . (Dlaczego właśnie  bity? Wynika to z uwagi powyżej.) bity? Wynika to z uwagi powyżej.)Następnie oblicza 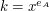 i wysyła do Antona i wysyła do Antona 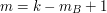 . .
Anton deszyfruje liczby
3.
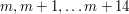 , podnosząc je do potęgi , podnosząc je do potęgi 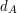 - otrzymując wartości - otrzymując wartości 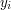 : : 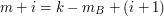 , , 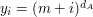 Następnie generuje pewną 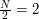 -bitową liczbę pierwszą -bitową liczbę pierwszą  taką, że wszystkie wartości taką, że wszystkie wartości 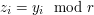 różnią się przynajmniej o 2. różnią się przynajmniej o 2.W kolejnym kroku Anton wysyła do Billa zestaw: 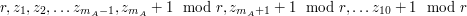 . - czyli zaznacza swój stan posiadania, zwiększając o . - czyli zaznacza swój stan posiadania, zwiększając o  ( (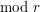 ) duże odszyfrowane wartości. ) duże odszyfrowane wartości.
Bill patrzy na 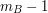 -szą z ciągu liczb otrzymanych za -szą z ciągu liczb otrzymanych za  . .Jeśli liczba ta jest równa 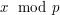 , to uznaje, że , to uznaje, że 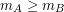 i odpowiedzią jest i odpowiedzią jest  . .W przeciwnym razie dochodzi do wniosku, że 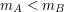 i odpowiedzią jest i odpowiedzią jest  . .Wysyła uznaną za poprawną odpowiedź do Antona. Dlaczego protokół jest bezpieczny i skąd Bill wie, kto ma więcej? Po pierwszym kroku Anton otrzymuje 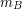 zaciemnione losową informacją, nie jest więc w stanie powiedzieć nic na jego temat. Jest to jedyny moment, w którym Anton otrzymuje od Billa jakąkolwiek wiadomość zawierającą zaciemnione losową informacją, nie jest więc w stanie powiedzieć nic na jego temat. Jest to jedyny moment, w którym Anton otrzymuje od Billa jakąkolwiek wiadomość zawierającą 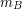 - zatem nie ma on szans poznać stanu konta konkurenta. - zatem nie ma on szans poznać stanu konta konkurenta.Co z Billem? W przedstawionej wersji może oszukiwać w ostatnim kroku, ale żeby dowiedzieć się dzięki temu, kto jest bogatszy, musiałby powtarzać protokół kilkukrotnie - na to Anton się nie nabierze! Czy gdzieś jeszcze uda się Billowi wywnioskować coś o nie swoim stanie konta? Anton wysyła do niego 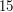 różnych liczb (różnych, bo każde dwie różniły się o przynajmniej różnych liczb (różnych, bo każde dwie różniły się o przynajmniej 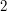 , a do niektórych przed wysłaniem dodaliśmy , a do niektórych przed wysłaniem dodaliśmy  ). Wystarczy, żeby miliarder potrafił ustalić, od której liczby zaczyna się ciąg zwiększony o ). Wystarczy, żeby miliarder potrafił ustalić, od której liczby zaczyna się ciąg zwiększony o  . Dlaczego nie jest to proste? Przeliczmy to (jeśli nie pamiętasz oznaczeń, cofnij się do opisu prookołu): . Dlaczego nie jest to proste? Przeliczmy to (jeśli nie pamiętasz oznaczeń, cofnij się do opisu prookołu):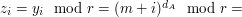 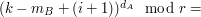 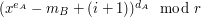 . .Bill, nie znając klucza prywatnego 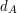 , nie jest w stanie zrobić nic, poza znalezieniem swojej liczby, , nie jest w stanie zrobić nic, poza znalezieniem swojej liczby,  . .Tę ostatnią może odtworzyć, ponieważ 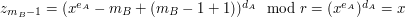 . Jeśli zatem . Jeśli zatem 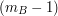 -sza liczba była równa -sza liczba była równa  (a nie (a nie 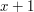 ), to ), to 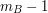 < < 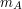 , czyli , czyli 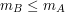 . .
Zamiast zakończeniaRozwiązaliśmy dwa całkiem życiowe problemy. Oczywiście, im więcej wiemy, tym więcej nasuwa się pytań - czy da się policzyć w podobny sposób każdą funkcję? Jak wydajne będą to obliczenia? Czy obliczenia w parach są dużo prostsze, niż w większych grupach? I właściwie - czy to ma jakieś praktyczne zastosowania? Wstrzymamy się na chwilę i nie odkryjemy jeszcze wszystkich kart, ale do tematu na pewno wrócimy. Powiedzmy na razie tylko, że odpowiedź na ostatnie pytanie jest pozytywna. Shafi Goldwasser, jedna z bardziej zasłużonych dla kryptografii osób na świecie, powiedziała kiedyś, że MPC jest w miejscu, gdzie 15-20 lat temu było szyfrowanie RSA; mechanizm ten faktycznie wydaje się być bardzo silny i dawać ogromne możliwości, trzeba tylko dokładnie go zbadać. Zadanie sprawdzające
W problemie dwóch biznesmenów powiedzieliśmy, że Bill może ustalić, ile Anton ma na koncie, jeśli będzie powtarzać protokół. W jaki sposób mógłby to osiągnąć i jaka jest minimalna liczba powtórzeń, jeśli obaj panowie mają więcej niż
Niektóre obrazki w artykule pochodzą z wikipedii. (1 ocena) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


 miliardów dolarów?
miliardów dolarów?


