Zagadnienie znajdowania najkrótszej ścieżki jest dość często spotykane. Czasem widać je wprost, czasem jest jednak tylko małą częścią trudniejszego problemu, jednak niezbędną, by go rozwiązać. Dlatego dogłębne poznanie tego zagadnienia (oraz sposobu jego rozwiązania) jest bardzo ważne dla wszystkich, którzy chcieliby umieć rozwiązywać owe łatwe zadania, gdzie widać od razu, że wystarczy znaleźć najkrótszą drogę, a jeszcze ważniejsze dla tych, którzy chcieliby rozwiązywać te trochę trudniejsze zadania.
Problem
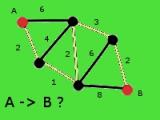
Rozważmy dostawcę, takiego normalnego człowieka, który ma samochód i musi przejechać z miasta  do miasta
do miasta  . Dysponuje on mapą, na której zaznaczone są wszystkie miejscowości w regionie, oraz zaznaczone jest, z której miejscowości do której można dojechać drogą nieprzechodzącą przez inną miejscowość (drogi krzyżują się tylko w miastach, między nimi omijają się tunelami czy estakadami). Kierowca jest zmęczony i chce jak najszybciej wrócić do domu, pytamy więc zatem jaka jest najkrótsza droga z miasta
. Dysponuje on mapą, na której zaznaczone są wszystkie miejscowości w regionie, oraz zaznaczone jest, z której miejscowości do której można dojechać drogą nieprzechodzącą przez inną miejscowość (drogi krzyżują się tylko w miastach, między nimi omijają się tunelami czy estakadami). Kierowca jest zmęczony i chce jak najszybciej wrócić do domu, pytamy więc zatem jaka jest najkrótsza droga z miasta  do miasta
do miasta  .
.
Dlaczego nie BFS?
Gdyby wszystkie bezpośrednie drogi pomiędzy miastami miały tą samą długość, to całą tą mapę można by przedstawić jako zwykły graf o krawędziach jednostkowych, i znaleźć tą najkrótszą ścieżkę algorytmem BFS. Co jeśli jednak drogi te nie są tej samej długości?
Można by podzielić te drogi na pewne odcinki, tak, żeby każda droga składała się z kilku odcinków, wszystkich tej samej długości. Wtedy na dłuższych drogach można by ustawić kilka "sztucznych miast" tak, żeby każde dwa miasta łączyły się drogą o tej samej długości i użyć BFS-a. Co jeśli jednak drogi są długie i takich miast trzeba by wstawić bardzo dużo? Algorytm BFS nie jest jednak zbyt skutecznym sposobem rozwiązywania tego problemu.
Algorytm Dijkstry
Rozważmy tą mapę jako graf ważony, tzn. wierzchołkom przypiszmy miasta, krawędziom pomiędzy wierzchołkami (miastami) wagi równe długościom dróg pomiędzy nimi. BFS jest bezużyteczny (może znaleźć drogę przez najmniejszą ilość miast), ale można skorzystać z
algorytmu Dijkstry. Pozwala on właśnie na znalezienie odległości wszystkich miast na takiej mapie od miasta  (warunkiem jest to, by wagi krawędzi były nieujemne). W szczególności pozwala nam również obliczyć odległość do miasta
(warunkiem jest to, by wagi krawędzi były nieujemne). W szczególności pozwala nam również obliczyć odległość do miasta  .
.
Wyobraźmy sobie, ze jesteśmy w mieście  . To co w tej chwili wiemy, to tyle, że nie musimy się nigdzie ruszać, aby dojechać do miasta
. To co w tej chwili wiemy, to tyle, że nie musimy się nigdzie ruszać, aby dojechać do miasta  , zatem można powiedzieć, że znajdujemy się w odległości 0 od miasta
, zatem można powiedzieć, że znajdujemy się w odległości 0 od miasta  . Poza tym z mapy możemy odczytać, w jakiej odległości znajdują się miasta połączone bezpośrednią drogą z
. Poza tym z mapy możemy odczytać, w jakiej odległości znajdują się miasta połączone bezpośrednią drogą z  . Popatrzmy teraz na miasto, które jest najbliżej. Nazwijmy je
. Popatrzmy teraz na miasto, które jest najbliżej. Nazwijmy je  . Patrząc na nie tak dokładniej można dojść do wniosku, że istotnie długość drogi z
. Patrząc na nie tak dokładniej można dojść do wniosku, że istotnie długość drogi z  do
do  jest odległością miasta
jest odległością miasta  od miasta
od miasta  .
.
Dowód
Gdyby tak nie było, to musiałoby istnieć taka droga poprzez inne miasta, że byłaby krótsza od bezpośredniej drogi z  do
do  (może być równa, ale to nie zmieniłoby faktu, że ta, którą wybraliśmy nadal jest jedną z najkrótszych). Ponieważ drogi mają nieujemne długości, to musiałoby istnieć jakieś miasto
(może być równa, ale to nie zmieniłoby faktu, że ta, którą wybraliśmy nadal jest jedną z najkrótszych). Ponieważ drogi mają nieujemne długości, to musiałoby istnieć jakieś miasto  sąsiadujące z
sąsiadujące z  , przez które ta droga by szła. Ponieważ sumarycznie droga ta ma być krótsza niż bezpośrednia droga z
, przez które ta droga by szła. Ponieważ sumarycznie droga ta ma być krótsza niż bezpośrednia droga z  do
do  , to żadna jej część składowa nie może być dłuższa niż długość bezpośredniej drogi z
, to żadna jej część składowa nie może być dłuższa niż długość bezpośredniej drogi z  do
do  , zatem długość drogi z
, zatem długość drogi z  do
do  musiałaby być mniejsza niż z
musiałaby być mniejsza niż z  do
do  . To jest sprzeczne z tym, że miasto
. To jest sprzeczne z tym, że miasto  wybraliśmy jako to, które jest najbliżej od miasta
wybraliśmy jako to, które jest najbliżej od miasta  .
.
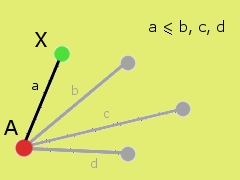
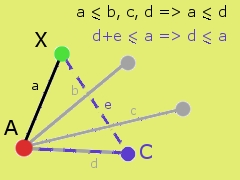
Rozumowanie takie można oczywiście rozszerzyć... mamy teraz 2 miasta, wiemy, że z miasta  do
do  najkrótsza ścieżka ma jakąś długość. Nazwijmy ją jakoś (tą długość), niech będzie
najkrótsza ścieżka ma jakąś długość. Nazwijmy ją jakoś (tą długość), niech będzie  . Zatem wiadomo, że do każdego z sąsiadów
. Zatem wiadomo, że do każdego z sąsiadów 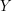 (tak sobie nazwijmy sąsiada
(tak sobie nazwijmy sąsiada  )miasta
)miasta  możemy dojechać z miasta
możemy dojechać z miasta  jakąś drogą złożoną z dwóch fragmentów: droga z miasta
jakąś drogą złożoną z dwóch fragmentów: droga z miasta  do
do  oraz z
oraz z  do
do 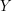 . Można zatem potraktować
. Można zatem potraktować 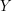 jako sąsiada
jako sąsiada  połączonego drogą o długości (
połączonego drogą o długości ( + długość drogi z
+ długość drogi z  do
do 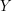 ). Popatrzmy teraz na takich "sąsiadów" miasta
). Popatrzmy teraz na takich "sąsiadów" miasta  .
.
Weźmy teraz najbliższego z nich (poza miastem  , bo dla niego znamy już ostateczną odpowiedź) i wybierzmy najbliższego z nich. Nazwijmy to miasto
, bo dla niego znamy już ostateczną odpowiedź) i wybierzmy najbliższego z nich. Nazwijmy to miasto 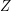 . Jak się tak głębiej zastanowić nad miastem
. Jak się tak głębiej zastanowić nad miastem 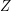 , to znów możemy powiedzieć, że odległość tego miasta od
, to znów możemy powiedzieć, że odległość tego miasta od  jest długością drogi z
jest długością drogi z  do
do 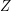 (tym razem już niekoniecznie bezpośredniej, może być to równie dobrze droga przez
(tym razem już niekoniecznie bezpośredniej, może być to równie dobrze droga przez  ).
).
Kłopotliwe miasto
Z jednym małym wyjątkiem... co jeśli w ten sposób wybraliśmy miasto  ? Otóż aby temu zapobiec musimy przestać traktować miasto
? Otóż aby temu zapobiec musimy przestać traktować miasto  (dla którego znamy już odpowiedź) jako sąsiada miasta
(dla którego znamy już odpowiedź) jako sąsiada miasta  , gdyż droga z miasta
, gdyż droga z miasta  do miasta
do miasta  przez jakieś inne miasto na pewno nie może mieć długości mniejszej niż 0 (więc w ten sposób nie uzyskamy lepszej odpowiedzi).
przez jakieś inne miasto na pewno nie może mieć długości mniejszej niż 0 (więc w ten sposób nie uzyskamy lepszej odpowiedzi).
Skoro już przebrnęliśmy przez ten wyjątek jesteśmy pewni że odległość miasta 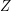 od
od  to długość ścieżki z
to długość ścieżki z 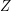 do
do  . Można to udowodnić w analogiczny sposób jak dla miasta
. Można to udowodnić w analogiczny sposób jak dla miasta  (zakładając że istnieje taka ścieżka i dochodząc do sprzeczności z tym, że
(zakładając że istnieje taka ścieżka i dochodząc do sprzeczności z tym, że 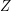 jest w tej chwili najbliższym interesującym nas "sąsiadem" miasta
jest w tej chwili najbliższym interesującym nas "sąsiadem" miasta  ).
).
Rozumowanie to jest jak na razie zadowalające i zapewne można je nadal rozszerzać.




 do miasta
do miasta  . Dysponuje on mapą, na której zaznaczone są wszystkie miejscowości w regionie, oraz zaznaczone jest, z której miejscowości do której można dojechać drogą nieprzechodzącą przez inną miejscowość (drogi krzyżują się tylko w miastach, między nimi omijają się tunelami czy estakadami). Kierowca jest zmęczony i chce jak najszybciej wrócić do domu, pytamy więc zatem jaka jest najkrótsza droga z miasta
. Dysponuje on mapą, na której zaznaczone są wszystkie miejscowości w regionie, oraz zaznaczone jest, z której miejscowości do której można dojechać drogą nieprzechodzącą przez inną miejscowość (drogi krzyżują się tylko w miastach, między nimi omijają się tunelami czy estakadami). Kierowca jest zmęczony i chce jak najszybciej wrócić do domu, pytamy więc zatem jaka jest najkrótsza droga z miasta  . Patrząc na nie tak dokładniej można dojść do wniosku, że istotnie długość drogi z
. Patrząc na nie tak dokładniej można dojść do wniosku, że istotnie długość drogi z  sąsiadujące z
sąsiadujące z 

 . Zatem wiadomo, że do każdego z sąsiadów
. Zatem wiadomo, że do każdego z sąsiadów 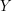 (tak sobie nazwijmy sąsiada
(tak sobie nazwijmy sąsiada 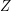 . Jak się tak głębiej zastanowić nad miastem
. Jak się tak głębiej zastanowić nad miastem 

