Indukcja
Załóżmy, że mamy policzoną taką drogę dla pewnej grupy miast (białe miasta). Powiedzmy, że jest tych miast  oraz ponumerujmy je od 1 do
oraz ponumerujmy je od 1 do  . Miastu
. Miastu  dajmy numer 1 (oznaczenia te mam nadzieję pomogą ogarnąć całą tą indukcję) teraz każdemu sąsiadowi (czerwony zbiór)
dajmy numer 1 (oznaczenia te mam nadzieję pomogą ogarnąć całą tą indukcję) teraz każdemu sąsiadowi (czerwony zbiór)  -tego miasta przypiszmy jakąś odległość od miasta 1. Będzie to najkrótsza droga po białych miastach, powiedzmy, że ma długość
-tego miasta przypiszmy jakąś odległość od miasta 1. Będzie to najkrótsza droga po białych miastach, powiedzmy, że ma długość  . Możemy go teraz traktować jako "sąsiada"
. Możemy go teraz traktować jako "sąsiada"  oddalonego o
oddalonego o  i umieścić z tą odległością w czerwonym zbiorze. Weźmy teraz miasto o najmniejszej odległości od
i umieścić z tą odległością w czerwonym zbiorze. Weźmy teraz miasto o najmniejszej odległości od  (niebieskie), takie, które nie jest żadnym z miast ponumerowanych od 1 do
(niebieskie), takie, które nie jest żadnym z miast ponumerowanych od 1 do  , nazwijmy go
, nazwijmy go 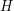 . Jeśli się przyjrzeć tak bliżej temu miastu, to najkrótsza droga z miasta
. Jeśli się przyjrzeć tak bliżej temu miastu, to najkrótsza droga z miasta  do
do 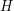 ma właśnie taką długość jak obecnie obliczana droga z
ma właśnie taką długość jak obecnie obliczana droga z  do
do 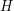 .
.
Dowód analogiczny (nie wprost)
Dowieść można tego analogicznie jak wcześniej dla miast  i
i  . załóżmy, że istnieje inna droga do
. załóżmy, że istnieje inna droga do 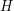 . jeśli prowadzi tylko przez miasta, które należą do białej grupy to znaleźlibyśmy właśnie tą drogę (bo jest krótsza), a jeśli prowadzi przez jakieś kolorowe miasto, to do tego miasta, przez które ta droga prowadzi, moglibyśmy dotrzeć krótszą drogą niż do
. jeśli prowadzi tylko przez miasta, które należą do białej grupy to znaleźlibyśmy właśnie tą drogę (bo jest krótsza), a jeśli prowadzi przez jakieś kolorowe miasto, to do tego miasta, przez które ta droga prowadzi, moglibyśmy dotrzeć krótszą drogą niż do 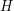 . Jednak zdefiniowaliśmy
. Jednak zdefiniowaliśmy 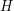 jako miasto, do którego można dotrzeć najkrótszą ścieżką z
jako miasto, do którego można dotrzeć najkrótszą ścieżką z  , które jeszcze nie zostało ponumerowane, więc nie może istnieć miasto kolorowe, do którego można dotrzeć krótszą drogą. Zatem długość drogi którą obecnie mamy policzoną z wierzchołka
, które jeszcze nie zostało ponumerowane, więc nie może istnieć miasto kolorowe, do którego można dotrzeć krótszą drogą. Zatem długość drogi którą obecnie mamy policzoną z wierzchołka  do
do 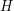 faktycznie jest najkrótszą (jedną z najkrótszych) ścieżek z miasta
faktycznie jest najkrótszą (jedną z najkrótszych) ścieżek z miasta  do
do 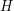 .
.
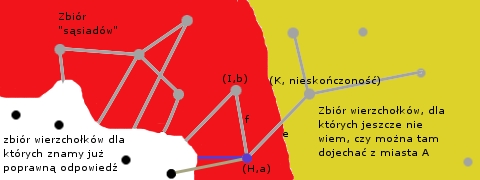
Zatem mam kolejne 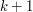 białe miasto do którego znam moją odległość, a do zbioru czerwonych "sąsiadów" mogę dorzucić wszystkich bezpośrednich sąsiadów
białe miasto do którego znam moją odległość, a do zbioru czerwonych "sąsiadów" mogę dorzucić wszystkich bezpośrednich sąsiadów 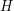 z odległością &m& od
z odległością &m& od  równą sumie odległości od
równą sumie odległości od  do
do 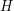 i długości bezpośredniej drogi do
i długości bezpośredniej drogi do 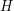 . Nie ma sensu jednak wrzucać od razu wszystkich bez namysłu. Jeśli popatrzę na takiego bezpośredniego sąsiada
. Nie ma sensu jednak wrzucać od razu wszystkich bez namysłu. Jeśli popatrzę na takiego bezpośredniego sąsiada 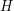 (nazwę go
(nazwę go 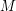 ) to nie zawsze warto go wrzucać do zbioru "sąsiadów".
) to nie zawsze warto go wrzucać do zbioru "sąsiadów".
-Jeżeli 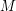 należy do zbioru białych wierzchołków to nigdy nie musimy go wrzucać do czerwonych "sąsiadów", bo znamy już dla niego odpowiedź (czyli na pewno jest nie gorsza od naszej propozycji).
należy do zbioru białych wierzchołków to nigdy nie musimy go wrzucać do czerwonych "sąsiadów", bo znamy już dla niego odpowiedź (czyli na pewno jest nie gorsza od naszej propozycji).
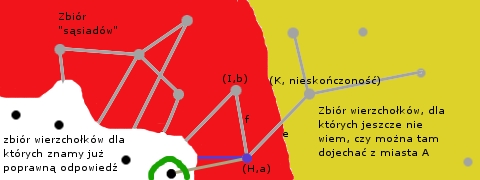
-Jeżeli 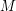 należy do zbioru czerwonych "sąsiadów" to musimy porównać długość drogi, którą mieliśmy dla niego już wcześniej z tą prowadzącą przez wierzchołek
należy do zbioru czerwonych "sąsiadów" to musimy porównać długość drogi, którą mieliśmy dla niego już wcześniej z tą prowadzącą przez wierzchołek 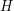 i wybrać krótszą z nich jako kandydata na odległość od wierzchołka
i wybrać krótszą z nich jako kandydata na odległość od wierzchołka  .
.
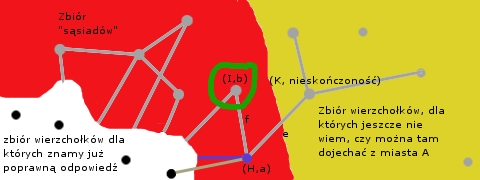
-W pozostałych przypadkach nie mieliśmy propozycji odpowiedzi dla 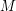 , więc wrzucamy
, więc wrzucamy 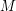 do czerwonych "sąsiadów" z odległością, którą policzyliśmy przez
do czerwonych "sąsiadów" z odległością, którą policzyliśmy przez 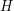 .
.
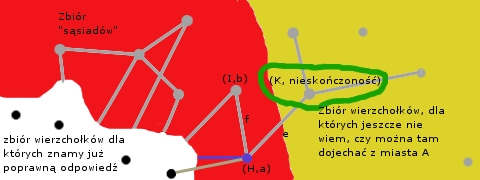
Możemy teraz postępować dalej, gdyż mamy 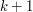 miast o tej samej własności (odpowiedzi dla nich są poprawne) oraz pewien zbiór czerwonych "sąsiadów".
miast o tej samej własności (odpowiedzi dla nich są poprawne) oraz pewien zbiór czerwonych "sąsiadów".
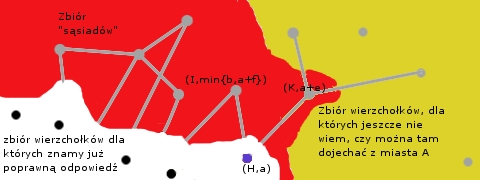
Jeśli nie ma już żadnych miast w zbiorze czerwonych "sąsiadów", dla których moglibyśmy obliczyć odległość, to nie ma już żadnych miast do których w ogóle możemy dojechać. Zatem obliczyliśmy drogi dla wszystkich miast, do których da się dojechać.
Otóż na samym początku aby uzyskać pewną spójność w całości rozumowania możemy powiedzieć, że ponumerowanych mamy 0 miast, jedynym znanym nam sąsiadem jest samo miasto  w odległości 0.Warto też mieć jakąś tablicę zawierającą odpowiedzi. Dla miasta
w odległości 0.Warto też mieć jakąś tablicę zawierającą odpowiedzi. Dla miasta  możemy od razu wpisać 0. O wszystkich pozostałych miastach nie wiemy, czy jest możliwość dojechania tam, czy nie, możemy myśleć o nich, że znajdują się nieskończenie daleko od naszego miasta (co z pewnych przyczyn jest wygodne później), więc do tabliczy odpowiedzi możemy im wpisać jakąś dużą liczbę udającą nieskończoność.
możemy od razu wpisać 0. O wszystkich pozostałych miastach nie wiemy, czy jest możliwość dojechania tam, czy nie, możemy myśleć o nich, że znajdują się nieskończenie daleko od naszego miasta (co z pewnych przyczyn jest wygodne później), więc do tabliczy odpowiedzi możemy im wpisać jakąś dużą liczbę udającą nieskończoność.




 oraz ponumerujmy je od 1 do
oraz ponumerujmy je od 1 do  dajmy numer 1 (oznaczenia te mam nadzieję pomogą ogarnąć całą tą indukcję) teraz każdemu sąsiadowi (czerwony zbiór)
dajmy numer 1 (oznaczenia te mam nadzieję pomogą ogarnąć całą tą indukcję) teraz każdemu sąsiadowi (czerwony zbiór)  -tego miasta przypiszmy jakąś odległość od miasta 1. Będzie to najkrótsza droga po białych miastach, powiedzmy, że ma długość
-tego miasta przypiszmy jakąś odległość od miasta 1. Będzie to najkrótsza droga po białych miastach, powiedzmy, że ma długość 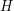 . Jeśli się przyjrzeć tak bliżej temu miastu, to najkrótsza droga z miasta
. Jeśli się przyjrzeć tak bliżej temu miastu, to najkrótsza droga z miasta  . załóżmy, że istnieje inna droga do
. załóżmy, że istnieje inna droga do 
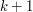 białe miasto do którego znam moją odległość, a do zbioru czerwonych "sąsiadów" mogę dorzucić wszystkich bezpośrednich sąsiadów
białe miasto do którego znam moją odległość, a do zbioru czerwonych "sąsiadów" mogę dorzucić wszystkich bezpośrednich sąsiadów  ) to nie zawsze warto go wrzucać do zbioru "sąsiadów".
) to nie zawsze warto go wrzucać do zbioru "sąsiadów". 





