Algorytm Dijkstry
25.11.2009 - Krzysztof Nowicki
  Zadania
Dostawca
Limit czasowy: 4s; Limit pamięciowy: 64 MB; Dostawca Kazimierz zajmuje się dostarczaniem, nie jest jednak bezpośrednim dostarczycielem, ale zajmuje się koordynowaniem. Do jego zadań należy znajdowanie najkrótszych dróg dla kierowców. Pan Kazimierz dysponuje mapą oraz opisem transportów (w którym mieście jest kierowca i do którego miasta ma coś zawieźć). Pomóż pamu Kazimierzowi znaleźć najkrótsze drogi dla dostawców mając opis mapy oraz transportów. Wejście:W pierwszej linii podane są dwie liczby W kolejnym wierszu znajduje się Wyjście:Skłąda się z Przykład: Dla wejścia: 8 15 Poprawne wyjście to: 13 Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany. Zaloguj się lub załóż konto.
Możliwości
Limit czasowy: 4s; Limit pamięciowy: 64MB; Nadworny geograf króla Mieczysława dostał bardzo nietypowe zadanie. Mianowicie król wymyślił sobie, że chce wiedzieć, jaka jest najkrótsza długość drogi ze stolicy do pewnego miasta. To jednak nie wszystko, co król chciałby wiedzieć od swojego geografa, potrzebna mu jest równiez ilość najkrótszych dróg ze stolicy do owego miasta.modulo pewną liczbę dodatnią Wejście:W pierwszej linii podane są dwie liczby W kolejnym wierszu znajduje się numer miasta Wyjście:Jeśli droga nie istnieje poprawnym wyjściem jest "INF". w przeciwnym wypadku w pierwszej linii powinna się znajdować długość najkrótszej drogi ze stolicy do miasta
Przykład: Dla wejścia: 8 15 Poprawne wyjście to: 10 Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany. Zaloguj się lub załóż konto.
(10 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


 <1001 i
<1001 i  oznaczające ilość miast oraz ilość połączeń między nimi. W kolejnych
oznaczające ilość miast oraz ilość połączeń między nimi. W kolejnych  ,
, , oraz
, oraz  oznaczające, że pomiędzy miastami
oznaczające, że pomiędzy miastami  <100 liczba transportów dla których pan Kazimierz chce znać najkrótszą drogę. W kolejnych
<100 liczba transportów dla których pan Kazimierz chce znać najkrótszą drogę. W kolejnych 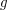 ,
,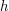 , które ozanczają, że transport ma dotrzeć z miasta
, które ozanczają, że transport ma dotrzeć z miasta  -tej długość najkrótszej drogi pomiędzy miastami z
-tej długość najkrótszej drogi pomiędzy miastami z  <1001. Aby geograf nie czuł się niepotrzebny król kazał mu również podać jedną z najkrótszych dróg ze stolicy do owego miasta. Na dodatek nie byle jaką, tylko taką, która jest odpowiednia, mianowicie król wjeżdżając do miasta chce wjeżdżać do niego z sąsiedniego miasta o najmniejszym możliwym numerze. Priorytetem jednak pozostaje to, aby droga była możliwie najkrótsza. Jako, że geograf jest tylko geografem, ma marne szanse aby wywiązać się z zadania samodzielnie. Pomóż ocalić mu głowę i napisz dla niego program, który dla podanego opisu mapy obliczy długość najkrótszej ścieżki do pewnego miasta, ilość najkrótszych ścieżek modulo
<1001. Aby geograf nie czuł się niepotrzebny król kazał mu również podać jedną z najkrótszych dróg ze stolicy do owego miasta. Na dodatek nie byle jaką, tylko taką, która jest odpowiednia, mianowicie król wjeżdżając do miasta chce wjeżdżać do niego z sąsiedniego miasta o najmniejszym możliwym numerze. Priorytetem jednak pozostaje to, aby droga była możliwie najkrótsza. Jako, że geograf jest tylko geografem, ma marne szanse aby wywiązać się z zadania samodzielnie. Pomóż ocalić mu głowę i napisz dla niego program, który dla podanego opisu mapy obliczy długość najkrótszej ścieżki do pewnego miasta, ilość najkrótszych ścieżek modulo  dla którego mamy obliczyć odległość ze stolicy (stolica ma numer 1) oraz liczba
dla którego mamy obliczyć odległość ze stolicy (stolica ma numer 1) oraz liczba 

