Wszędzie otaczają nas liczby: większe, mniejsze - żadnej reguły! Trzeba jednak to wszystko ogarnąć i znaleźć jakieś prawidłowości wśród nich. W tym artykule zajmiemy się znajdowaniem najdłuższego podciągu rosnącego, czyli światełko w tunelu dla tych, którzy nie lubią chaosu. Zapraszam do zabawy z liczbami!
Najdłuższy podciąg rosnący to, w języku wyspiarzy, Longest Ascending Sequence, więc będziemy pisali w skrócie po prostu LAS. Zastanówmy się najpierw, co znaczą:
- najdłuższy: Czyli nie ma dłuższych i tyle. Innymi słowy, chcemy znaleźć dowolny z najdłuższych LAS-ów.
- podciąg: Właśnie - co to jest podciąg? Mamy dany ciąg (liczb, liter, czegokolwiek):
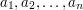 . Wtedy podciąg to dowolny ciąg
. Wtedy podciąg to dowolny ciąg 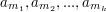 taki, że
taki, że 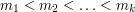 . Zatem nie jest to spójny fragment ciągu, ale jego niektóre elementy w oryginalnej kolejności.
. Zatem nie jest to spójny fragment ciągu, ale jego niektóre elementy w oryginalnej kolejności. - rosnący: w tym artykule przyjmujemy, że jest ściśle rosnący. Oczywiście, algorytmy zaprezentowane poniżej można bardzo łatwo zmodyfikować tak, żeby wyszukiwać równie dobrze ciągi malejące, nierosnące i niemalejące.
Dla klarowności zróbmy sobie jakiś przykład:
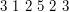
Tutaj LAS będzie miał długość 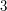 , ale są trzy podciagi rywalizujące o to miano:
, ale są trzy podciagi rywalizujące o to miano: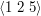 i
i 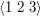 i
i 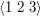 . Nie, to nie jest błąd - dwa ostatnie różnią się tym, którą dwójkę do nich wybraliśmy.
. Nie, to nie jest błąd - dwa ostatnie różnią się tym, którą dwójkę do nich wybraliśmy.
Zastanówmy się teraz, jak podejść ten problem z kilku stron.
Podejście grafowe
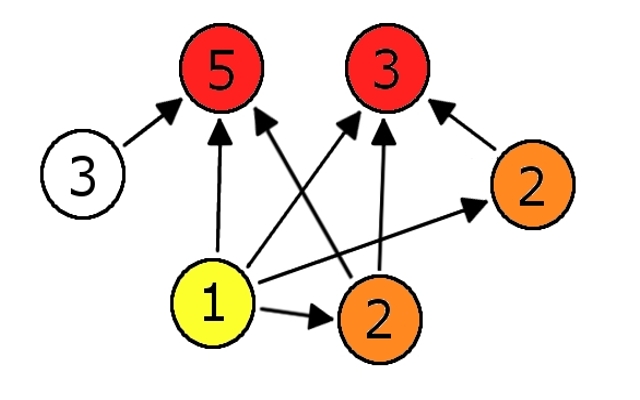 Ktoś mądry powiedział kiedyś: "wszystko jest grafem". Posłuchajmy więc mądrzejszych od siebie i zróbmy z tego ciągu graf. Jego wierzchołkami będą elementy, natomiast (skierowane) krawędzie narysujmy między takimi elementami
Ktoś mądry powiedział kiedyś: "wszystko jest grafem". Posłuchajmy więc mądrzejszych od siebie i zróbmy z tego ciągu graf. Jego wierzchołkami będą elementy, natomiast (skierowane) krawędzie narysujmy między takimi elementami 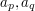 , że
, że 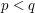 i
i  , czyli tworzącymi dwuelementowy podciąg rosnący. Jednym z pomysłów jest zrobienie takiego jakby BFSa. (Jeśli nie znasz tego algorytmu, gorąco polecam zapoznanie się z nim - niemniej jego znajomość nie jest tu konieczna).
, czyli tworzącymi dwuelementowy podciąg rosnący. Jednym z pomysłów jest zrobienie takiego jakby BFSa. (Jeśli nie znasz tego algorytmu, gorąco polecam zapoznanie się z nim - niemniej jego znajomość nie jest tu konieczna).
Jak w ogóle działa BFS? Zaczyna od pewnego wierzchołka i, z grubsza, dzieli graf na warstwy: do pierwszej wrzuca te wierzchołki, do których da się dojść ze startowego w jednym kroku, do następnej - te w odległości dwóch kroków itd. Gdyby więc udało się podzielić ten graf na warstwy nie po najkrótszych ścieżkach, ale po najdłuższych, zadanie byłoby rozwiązane. Na rysunku widać, co się stanie, gdybyśmy takiego zmodyfikowanego BFSa zaczęli od wierzchołka 1. Niestety nie wiemy, co zrobić z wierzchołkiem 3... Zachęcam do przemyślenia jeszcze tego pomysłu, ale moim zdaniem jest on nieco nietrafiony. Zostawmy więc te nieszczęsne grafy.
Podejście dynamiczne
(Rozwiązanie dynamiczne to takie, w którym do policzenia pewnej wartości używamy wartości policzonych już wcześniej). Proponuję taki algorytm: dla każdego elementu policzmy, jaki jest najdłuższy podciąg rosnący kończący się tym elementem.
Widzimy, że jeśli chcemy to policzyć dla pewnego elementu, to najpierw musimy mieć już wartości dla wszystkich poprzednich. Znając je, łatwo policzymy szukaną wartość - przeglądając wszystkich mniejszych poprzedników. Okazuje się, że to wystarcza - doskonale! Mamy więc poprawny i prosty do zaimplementowania algorytm szukający długość LASu:
int LongestEndingWith[n];
int Sequence[n];
int LongestEver = 0;
for (int i=0; i<n; i += 1) scanf(sequence[i]);
for (int i=0; i<n; i += 1)
LongestEndingWith[i] = 1;
/*LAS kończący się i-tym elementem ma długość przynajmniej 1*/
for (int j=0; j<i; j += 1)
if (Sequence[j] < Sequence[i])
LongestEndingWith[i] = max(LongestEndingWith[i], LongestEndingWith[j]+1);
/*Patrzymy na wszystkie elementy mniejsze od danego i tam szukamy podciągów,
biorąc maksimum ze wszystkich potencjalnych poprzedników
LongestEver = max(LongestEver, LongestEndingWith[i]);
/*zwracamy oczywiście maksimum ze wszystkich wartości*/
printf(LongestEver);
Ten algorytm działa w czasie 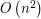 (czemu? gdyż dla każdego elementu przejrzymy wszystkie poprzednie, czyli łącznie wykonamy
(czemu? gdyż dla każdego elementu przejrzymy wszystkie poprzednie, czyli łącznie wykonamy 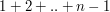 porównań, co daje czas kwadratowy). Okazuje się jednak, że nie jest to najlepszy wynik. Spróbujmy zmodyfikować powyższy algorytm korzystając z "BFS-owego" spostrzeżenia - podzielmy ciąg na "warstwy". Jak sie domyślamy, w
porównań, co daje czas kwadratowy). Okazuje się jednak, że nie jest to najlepszy wynik. Spróbujmy zmodyfikować powyższy algorytm korzystając z "BFS-owego" spostrzeżenia - podzielmy ciąg na "warstwy". Jak sie domyślamy, w  -tej warstwie będą wszystkie takie wyrazy, dla których najdłuższy podciąg rosnący kończący się na nim ma długość
-tej warstwie będą wszystkie takie wyrazy, dla których najdłuższy podciąg rosnący kończący się na nim ma długość  .
.
Intuicyjnie, każda kolejna warstwa będzie zawierała, w pewnym sensie, "większe" elementy niż poprzednia, zatem żeby znaleźć wszystkie elementy mniejsze od danego, przejrzymy tylko kilka pierwszych warstw. Widzimy wiec szansę zastosowania jakiegoś binary-searcha... I o to chodzi w tym algorytmie. (Temu, kto nie zna binary-searcha, radzę zrobić sobie przerwę w lekturze niniejszego tekstu i przeczytać artykuł o tym algorytmie, również w dziale "Zostań Zawodnikiem")





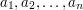 . Wtedy podciąg to dowolny ciąg
. Wtedy podciąg to dowolny ciąg 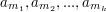 taki, że
taki, że 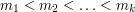 . Zatem nie jest to spójny fragment ciągu, ale jego niektóre elementy w oryginalnej kolejności.
. Zatem nie jest to spójny fragment ciągu, ale jego niektóre elementy w oryginalnej kolejności.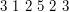
 , ale są trzy podciagi rywalizujące o to miano:
, ale są trzy podciagi rywalizujące o to miano: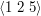 i
i 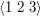 i
i  Ktoś mądry powiedział kiedyś: "wszystko jest grafem". Posłuchajmy więc mądrzejszych od siebie i zróbmy z tego ciągu graf. Jego wierzchołkami będą elementy, natomiast (skierowane) krawędzie narysujmy między takimi elementami
Ktoś mądry powiedział kiedyś: "wszystko jest grafem". Posłuchajmy więc mądrzejszych od siebie i zróbmy z tego ciągu graf. Jego wierzchołkami będą elementy, natomiast (skierowane) krawędzie narysujmy między takimi elementami 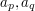 , że
, że 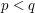 i
i 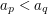 , czyli tworzącymi dwuelementowy podciąg rosnący. Jednym z pomysłów jest zrobienie takiego jakby BFSa. (Jeśli nie znasz tego algorytmu, gorąco polecam zapoznanie się z nim - niemniej jego znajomość nie jest tu konieczna).
, czyli tworzącymi dwuelementowy podciąg rosnący. Jednym z pomysłów jest zrobienie takiego jakby BFSa. (Jeśli nie znasz tego algorytmu, gorąco polecam zapoznanie się z nim - niemniej jego znajomość nie jest tu konieczna).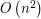 (czemu? gdyż dla każdego elementu przejrzymy wszystkie poprzednie, czyli łącznie wykonamy
(czemu? gdyż dla każdego elementu przejrzymy wszystkie poprzednie, czyli łącznie wykonamy 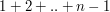 porównań, co daje czas kwadratowy). Okazuje się jednak, że nie jest to najlepszy wynik. Spróbujmy zmodyfikować powyższy algorytm korzystając z "BFS-owego" spostrzeżenia - podzielmy ciąg na "warstwy". Jak sie domyślamy, w
porównań, co daje czas kwadratowy). Okazuje się jednak, że nie jest to najlepszy wynik. Spróbujmy zmodyfikować powyższy algorytm korzystając z "BFS-owego" spostrzeżenia - podzielmy ciąg na "warstwy". Jak sie domyślamy, w  -tej warstwie będą wszystkie takie wyrazy, dla których najdłuższy podciąg rosnący kończący się na nim ma długość
-tej warstwie będą wszystkie takie wyrazy, dla których najdłuższy podciąg rosnący kończący się na nim ma długość 

