Najdłuższy podciąg rosnący
25.11.2009 - Karol Konaszyński
  ZamekLimit czasowy: 8s, Limit pamięciowy: 32MB. Grasz w grę Zamek. W każdej turze możesz awansować swój zamek na pewien poziom i za każdy awans (nieważne o ile poziomów, ważne, że o co najmniej 1) dostajesz 1 punkt zwycięstwa. Udało ci się jednak podejrzeć pliki konfiguracyjne gry i wiesz, jakie będą kolejne poziomy, na które, w kolejnych turach, będzie można awansować zamek. Ponadto wiesz, że w Wejście 3 Poprawną odpowiedzią jest: 4 1 5 7 10 Wyjaśnienie: Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany. Zaloguj się lub załóż konto.
Badanie DNALimit czasowy: 8s, Limit pamięciowy: 32MB. Jesteś biologiem (biolożką) i badasz łańcuchy DNA. Twój zespół postanowił zająć się porównywaniem sekwencji DNA różnych gatunków małp oraz człowieka. Każda sekwencja DNA składa się, według was, z niewielkiej (kilka miliardów) ilości fragmentów, które często powtarzają się w DNA ssaków. Najprościej rzecz ujmując, DNA to ciąg fragmentów, z których każdy ma pewien numer. Ponadto te fragmenty są tak ustalone, że, jakimś cudem, genom człowieka składa się z różnych fragmentów (tzn. żaden się nie powtarza). Napisz program, który dla zadanych sekwencji DNA będzie porównywał je z DNA człowieka i wypisze, jaki jest ich najdłuższy wspólny podciąg fragmentów. 5 3 Poprawną odpowiedzią jest: 2 1 1 Wyjaśnienie do przykładu: Dla pierwszej sekwencji najdłuższy wspólny podciąg to, na przykład, 3 1, dla drugiej jednoelementowy 1, dla trzeciej tylko 2. Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany. Zaloguj się lub załóż konto.
KlockiLimit czasowy: 8s, Limit pamięciowy: 32MB. Bajtuś ma dwa hobby - układanie wież z klocków i bawienie się liczbami. Ostatnio na gwiazdkę dostał zestaw klocków, na których były napisane liczby. Tych klocków było sporo, więc ułożenie wieży z nich złożonej wymagało dużo czasu i koncentracji. Gdy mu się to w końcu udało, paradoksalnie poczuł się dość smutny - bo cóż innego mógł jeszcze z nimi zrobić? Ale w pewnym momencie, gdy patrzył na liczby napisane na klockach, przyszedł mu do głowy pomysł. Postanowił ostrożnie usunąć niektóre klocki z wieży tak, żeby jak najwięcej spośród pozostałych klocków było "fajnych", czyli znajdowało się na takiej wysokości, na jaką wskazuje liczba napisana na klocku (klocek leżący bezpośrednio na ziemi jest na wysokości 1, następny na wysokości 2 i tak dalej). Sprawdź, ile, w danej wieży, najwięcej klocków może być fajnych.
7 Poprawnym wyjściem jest: 3 Wyjaśnienie: Po usunięciu klocka drugiego wieża będzie wyglądała tak: Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany. Zaloguj się lub załóż konto. (15 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


 -tej turze wykorzystanie możliwości awansu kosztuje
-tej turze wykorzystanie możliwości awansu kosztuje 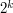 dukatów. Policz więc, ile punktów zwycięstwa uda ci się zdobyć. Jeśli masz więcej możliwości, wybierz tę o najmniejszym koszcie. (Zauważ, że im wcześniej się zdecydujesz na awans, tym lepiej!). Zaczynasz od poziomu 0.
dukatów. Policz więc, ile punktów zwycięstwa uda ci się zdobyć. Jeśli masz więcej możliwości, wybierz tę o najmniejszym koszcie. (Zauważ, że im wcześniej się zdecydujesz na awans, tym lepiej!). Zaczynasz od poziomu 0.
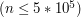 , a następnie
, a następnie 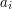
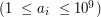 określające na jaki poziom możesz awansować zamek w
określające na jaki poziom możesz awansować zamek w  -tej turze.
-tej turze. oznaczającej ilość punktów zwycięstwa, które możesz uzyskać, a następnie
oznaczającej ilość punktów zwycięstwa, które możesz uzyskać, a następnie 
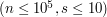 oznaczające odpowiednio: ilość fragmentów w DNA człowieka i ilość gatunków małp, których sekwencje chcesz rozpatrzyć. W następnej linii znajduje się
oznaczające odpowiednio: ilość fragmentów w DNA człowieka i ilość gatunków małp, których sekwencje chcesz rozpatrzyć. W następnej linii znajduje się 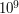 , czyli numerów fragmentów, które składają się na DNA człowieka. W każdej z
, czyli numerów fragmentów, które składają się na DNA człowieka. W każdej z 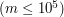 będącą długością kolejnej sekwencji i
będącą długością kolejnej sekwencji i 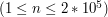 , ilość klocków w wieży. W kolejnej linii znajduje się
, ilość klocków w wieży. W kolejnej linii znajduje się 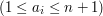 określających liczbę napisaną na i-tym klocku.
określających liczbę napisaną na i-tym klocku.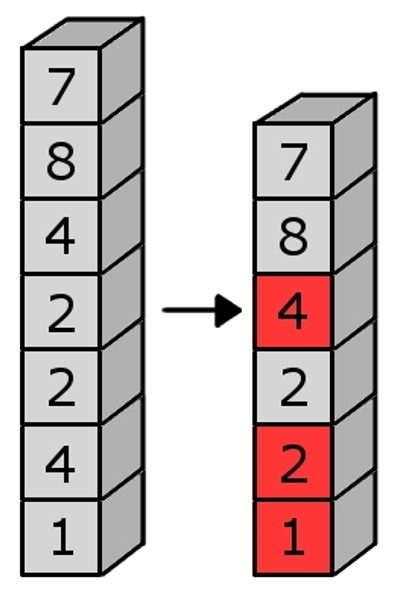
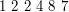 , czyli klocki o numerach 1, 2 i 4 będą na fajnych miejscach. Równie dobrze można też usunąć klocki 8 i 7. Gdybyśmy nic nie usuwali, byłyby dwa fajne klocki: 1 i 7.
, czyli klocki o numerach 1, 2 i 4 będą na fajnych miejscach. Równie dobrze można też usunąć klocki 8 i 7. Gdybyśmy nic nie usuwali, byłyby dwa fajne klocki: 1 i 7.

