Wielowymiarowy LAS
(Uwaga! Teraz nastąpi bardzo ważne spostrzeżenie!) Zauważmy, że ciąg 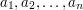 możemy reprezentować jako zbiór par
możemy reprezentować jako zbiór par 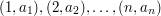 . Wtedy nie musimy bać się o kolejność i zadanie staje się następujące: Znaleźć największy podzbiór tego zbioru par o takiej własności, że z każdych dwóch elementów jeden jest "silnie większy" od drugiego, czyli ma obie współrzędne większe. Dlatego ten problem można nazwać 2-wymiarowym najdłuższym łańcuchem (2-dimensional Longest Chain - 2-DimLC).
. Wtedy nie musimy bać się o kolejność i zadanie staje się następujące: Znaleźć największy podzbiór tego zbioru par o takiej własności, że z każdych dwóch elementów jeden jest "silnie większy" od drugiego, czyli ma obie współrzędne większe. Dlatego ten problem można nazwać 2-wymiarowym najdłuższym łańcuchem (2-dimensional Longest Chain - 2-DimLC).
Jak może wyglądać 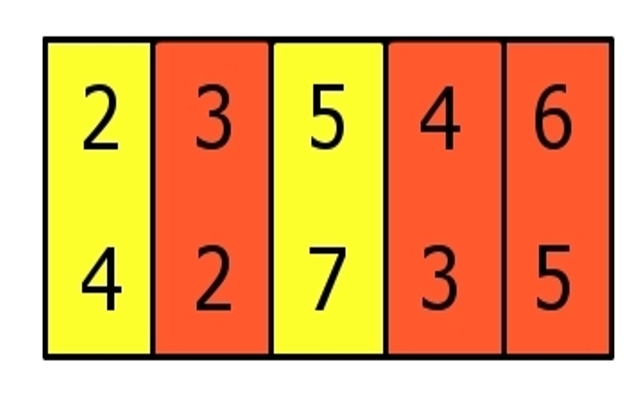 3-DimLC czyli 2-dimLAS? Dany jest zbiór trójek, czyli uporządkowany ciąg par
3-DimLC czyli 2-dimLAS? Dany jest zbiór trójek, czyli uporządkowany ciąg par 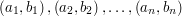 i chcemy w nim znaleźć najdłuższy podciąg silnie rosnący. Spójrzmy teraz na rysunek. Tutaj najdłuższy podciąg rosnący zaznaczony jest na czerwono: na obu współrzędnych jest ściśle rosnący. Jak się tego szuka? Jeden z algorytmów (ten, który ja znam...) działa podobnie jak w przypadku niżejwymiarowym, w szczególności warstwy są zdefiniowane tak samo (tzn. w
i chcemy w nim znaleźć najdłuższy podciąg silnie rosnący. Spójrzmy teraz na rysunek. Tutaj najdłuższy podciąg rosnący zaznaczony jest na czerwono: na obu współrzędnych jest ściśle rosnący. Jak się tego szuka? Jeden z algorytmów (ten, który ja znam...) działa podobnie jak w przypadku niżejwymiarowym, w szczególności warstwy są zdefiniowane tak samo (tzn. w  -tej znajdują się elementy kończące pewien podciąg o długości
-tej znajdują się elementy kończące pewien podciąg o długości  ). Problemem jest tylko to, że nie możemy za każdym razem wrzucać na listę elementu najmniejszego (bo nie można par uporządkować w ten sposób!). Nie możemy więc, w binary searchu, patrzeć na ostatni element listy.
). Problemem jest tylko to, że nie możemy za każdym razem wrzucać na listę elementu najmniejszego (bo nie można par uporządkować w ten sposób!). Nie możemy więc, w binary searchu, patrzeć na ostatni element listy.
Musimy więc niejako przeglądać całą warstwę. Gdy jednak zagwarantujemy, że jest ona posortowana np. rosnąco po pierwszej współrzędnej oraz malejąco po drugiej, to w obrębie warstwy możemy użyć kolejny raz binary-searcha. Czemu to w ogóle jest możliwe? Przyda się tutaj ważne spostrzeżenie: nie wszystkie elementy są potrzebne, więc po wrzuceniu jakiejś pary 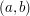 do warstwy możemy z niej usunąć wszystkie pary
do warstwy możemy z niej usunąć wszystkie pary 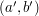 spełniające
spełniające 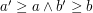 . Zatem w ogólności algorytm wygląda tak:
. Zatem w ogólności algorytm wygląda tak:
dla każdego kolejnego elementu:
- sprawdź binary searchem numer najdalszej warstwy, w której jest element silnie mniejszy od danego
- wrzuć go do warstwy następnej
- usuń elementy niepotrzebne (jak?).
Musimy jednak mieć jakąś strukturę, która umożliwi nam wykonywanie takich operacji. Do tego celu warto użyć jakiegoś drzewa (np seta z stl-a):
 Niestety, na wdawanie się w szczegóły botaniczno-implementacyjne nie ma tu miejsca, mamy bowiem jeszcze jedną rzecz do omówienia. Ale policzmy jeszcze złożoność obliczeniową tego algorytmu. Dla każdego elementu binary-searchuję go w ciągu warstw, ale każde sprawdzenie wymaga znowu binary-searcha po warstwie (
Niestety, na wdawanie się w szczegóły botaniczno-implementacyjne nie ma tu miejsca, mamy bowiem jeszcze jedną rzecz do omówienia. Ale policzmy jeszcze złożoność obliczeniową tego algorytmu. Dla każdego elementu binary-searchuję go w ciągu warstw, ale każde sprawdzenie wymaga znowu binary-searcha po warstwie (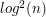 ). Następnie muszę go wstawić do tej warstwy, co też zajmie
). Następnie muszę go wstawić do tej warstwy, co też zajmie 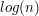 , a potem usunąć elementy niepotrzebne, co zajmie nam maksymalnie
, a potem usunąć elementy niepotrzebne, co zajmie nam maksymalnie 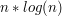 (jako że każdy element usuniemy co najwyżej raz) - czyli mamy
(jako że każdy element usuniemy co najwyżej raz) - czyli mamy 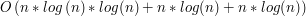 , co daje
, co daje 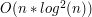 . Podobno, k-DimLC da się rozwiązać w czasie
. Podobno, k-DimLC da się rozwiązać w czasie 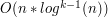 . Niestety, autor niniejszego artykułu nie ma pojęcia jak to zrobić...
. Niestety, autor niniejszego artykułu nie ma pojęcia jak to zrobić...
Teraz jeszcze jedna wariacja na temat:
Longest common subsequence
(Ten rodział jest przeznaczony dla tych, którzy znają ten problem, gdyż tutaj będziemy korzystać ze standardowego algorytmu)
Postawowy algorytm do wyszukiwania LCSa dwóch słów o długości 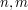 polega na utworzeniu tabelki
polega na utworzeniu tabelki 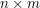 i wypełnieniu jej w pewien magiczny sposób, co zajmuje mu czas
i wypełnieniu jej w pewien magiczny sposób, co zajmuje mu czas 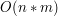 . Gdy jednak założymy, że w jednym z słów wszystkie literki sa różne (np. jakieś chińskie słowo), to problem sprowadza się do znalezienia najdłuższego podciągu rosnącego!
. Gdy jednak założymy, że w jednym z słów wszystkie literki sa różne (np. jakieś chińskie słowo), to problem sprowadza się do znalezienia najdłuższego podciągu rosnącego!
Otóż, każdej literce  słowa
słowa  (tego o różnych literach) przypiszmy jej indeks, czyli niech
(tego o różnych literach) przypiszmy jej indeks, czyli niech 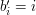 . Wtedy weźmy to pierwsze słowo
. Wtedy weźmy to pierwsze słowo 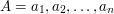 i dla każdej jego literki robimy tak: jeśli nie występuje w drugim słowie to ją "usuwamy" (czyli po prostu nie rozpatrujemy), zaś gdy występuje (czyli zachodzi
i dla każdej jego literki robimy tak: jeśli nie występuje w drugim słowie to ją "usuwamy" (czyli po prostu nie rozpatrujemy), zaś gdy występuje (czyli zachodzi 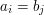 ), to wtedy zastępujemy ją przez
), to wtedy zastępujemy ją przez  , czyli indeks tej literki w słowie drugim. Mamy więc
, czyli indeks tej literki w słowie drugim. Mamy więc 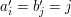 . Wtedy najdłuższy wspólny podciąg będzie najdłuższym podciągiem rosnącym dla nowego ciągu
. Wtedy najdłuższy wspólny podciąg będzie najdłuższym podciągiem rosnącym dla nowego ciągu 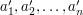 (teraz już nie słowa, a ciągu indeksów).
(teraz już nie słowa, a ciągu indeksów).
Czemu to działa? Dowód, oczywiście, pozostawiam czytelnikom! Ważne jest to, że potrafimy znaleźć LCS w czasie (w zależności od implementacji) 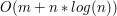 lub
lub 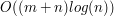 , gdzie
, gdzie  jest długością tego "zróżnicowanego" ciągu, czyli znacznie szybciej niż standardowy LCS. Do przemyślenia: co się stanie, gdy w tym drugim słowie każda z liter będzie występowała najwyżej
jest długością tego "zróżnicowanego" ciągu, czyli znacznie szybciej niż standardowy LCS. Do przemyślenia: co się stanie, gdy w tym drugim słowie każda z liter będzie występowała najwyżej  razy, gdzie
razy, gdzie  jest jakąś stałą (np.
jest jakąś stałą (np. 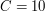 )? Czy potrafimy to rozwiązać w czasie
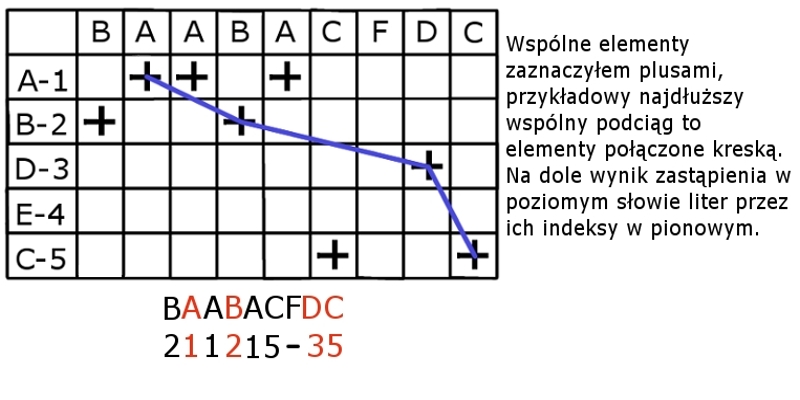
)? Czy potrafimy to rozwiązać w czasie 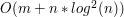 ?
?
Na tym kończymy rozważania na ten temat.
Przyznam szczerze, że problem jest nietrywialny i o ile sam w sobie nie jest aż tak przydatny jak np. drzewa przedziałowe, to idee z nim zwiazane przewijają się bardzo często (np zadanie Architekci, II etap XVI OI) i nierzadko w zakamuflowanej formie.
Poniżej przedstawiam trzy zadania. Dwa z nich polegają na zaimplementowaniu tego, co zostało opisane w niniejszym artykule, jedno jest przykładem takiego "kamuflażu". Miłej zabawy :D




 możemy reprezentować jako zbiór par
możemy reprezentować jako zbiór par 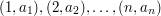 . Wtedy nie musimy bać się o kolejność i zadanie staje się następujące: Znaleźć największy podzbiór tego zbioru par o takiej własności, że z każdych dwóch elementów jeden jest "silnie większy" od drugiego, czyli ma obie współrzędne większe. Dlatego ten problem można nazwać 2-wymiarowym najdłuższym łańcuchem (2-dimensional Longest Chain - 2-DimLC).
. Wtedy nie musimy bać się o kolejność i zadanie staje się następujące: Znaleźć największy podzbiór tego zbioru par o takiej własności, że z każdych dwóch elementów jeden jest "silnie większy" od drugiego, czyli ma obie współrzędne większe. Dlatego ten problem można nazwać 2-wymiarowym najdłuższym łańcuchem (2-dimensional Longest Chain - 2-DimLC). 3-DimLC czyli 2-dimLAS? Dany jest zbiór trójek, czyli uporządkowany ciąg par
3-DimLC czyli 2-dimLAS? Dany jest zbiór trójek, czyli uporządkowany ciąg par 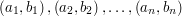 i chcemy w nim znaleźć najdłuższy podciąg silnie rosnący. Spójrzmy teraz na rysunek. Tutaj najdłuższy podciąg rosnący zaznaczony jest na czerwono: na obu współrzędnych jest ściśle rosnący. Jak się tego szuka? Jeden z algorytmów (ten, który ja znam...) działa podobnie jak w przypadku niżejwymiarowym, w szczególności warstwy są zdefiniowane tak samo (tzn. w
i chcemy w nim znaleźć najdłuższy podciąg silnie rosnący. Spójrzmy teraz na rysunek. Tutaj najdłuższy podciąg rosnący zaznaczony jest na czerwono: na obu współrzędnych jest ściśle rosnący. Jak się tego szuka? Jeden z algorytmów (ten, który ja znam...) działa podobnie jak w przypadku niżejwymiarowym, w szczególności warstwy są zdefiniowane tak samo (tzn. w  -tej znajdują się elementy kończące pewien podciąg o długości
-tej znajdują się elementy kończące pewien podciąg o długości 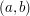 do warstwy możemy z niej usunąć wszystkie pary
do warstwy możemy z niej usunąć wszystkie pary 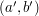 spełniające
spełniające 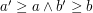 . Zatem w ogólności algorytm wygląda tak:
. Zatem w ogólności algorytm wygląda tak: Niestety, na wdawanie się w szczegóły botaniczno-implementacyjne nie ma tu miejsca, mamy bowiem jeszcze jedną rzecz do omówienia. Ale policzmy jeszcze złożoność obliczeniową tego algorytmu. Dla każdego elementu binary-searchuję go w ciągu warstw, ale każde sprawdzenie wymaga znowu binary-searcha po warstwie (
Niestety, na wdawanie się w szczegóły botaniczno-implementacyjne nie ma tu miejsca, mamy bowiem jeszcze jedną rzecz do omówienia. Ale policzmy jeszcze złożoność obliczeniową tego algorytmu. Dla każdego elementu binary-searchuję go w ciągu warstw, ale każde sprawdzenie wymaga znowu binary-searcha po warstwie (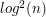 ). Następnie muszę go wstawić do tej warstwy, co też zajmie
). Następnie muszę go wstawić do tej warstwy, co też zajmie 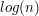 , a potem usunąć elementy niepotrzebne, co zajmie nam maksymalnie
, a potem usunąć elementy niepotrzebne, co zajmie nam maksymalnie 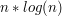 (jako że każdy element usuniemy co najwyżej raz) - czyli mamy
(jako że każdy element usuniemy co najwyżej raz) - czyli mamy 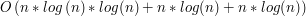 , co daje
, co daje 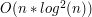 . Podobno, k-DimLC da się rozwiązać w czasie
. Podobno, k-DimLC da się rozwiązać w czasie 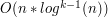 . Niestety, autor niniejszego artykułu nie ma pojęcia jak to zrobić...
. Niestety, autor niniejszego artykułu nie ma pojęcia jak to zrobić...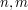 polega na utworzeniu tabelki
polega na utworzeniu tabelki 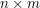 i wypełnieniu jej w pewien magiczny sposób, co zajmuje mu czas
i wypełnieniu jej w pewien magiczny sposób, co zajmuje mu czas 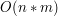 . Gdy jednak założymy, że w jednym z słów wszystkie literki sa różne (np. jakieś chińskie słowo), to problem sprowadza się do znalezienia najdłuższego podciągu rosnącego!
. Gdy jednak założymy, że w jednym z słów wszystkie literki sa różne (np. jakieś chińskie słowo), to problem sprowadza się do znalezienia najdłuższego podciągu rosnącego! słowa
słowa  (tego o różnych literach) przypiszmy jej indeks, czyli niech
(tego o różnych literach) przypiszmy jej indeks, czyli niech 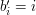 . Wtedy weźmy to pierwsze słowo
. Wtedy weźmy to pierwsze słowo 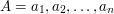 i dla każdej jego literki robimy tak: jeśli nie występuje w drugim słowie to ją "usuwamy" (czyli po prostu nie rozpatrujemy), zaś gdy występuje (czyli zachodzi
i dla każdej jego literki robimy tak: jeśli nie występuje w drugim słowie to ją "usuwamy" (czyli po prostu nie rozpatrujemy), zaś gdy występuje (czyli zachodzi 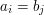 ), to wtedy zastępujemy ją przez
), to wtedy zastępujemy ją przez  , czyli indeks tej literki w słowie drugim. Mamy więc
, czyli indeks tej literki w słowie drugim. Mamy więc 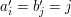 . Wtedy najdłuższy wspólny podciąg będzie najdłuższym podciągiem rosnącym dla nowego ciągu
. Wtedy najdłuższy wspólny podciąg będzie najdłuższym podciągiem rosnącym dla nowego ciągu 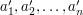 (teraz już nie słowa, a ciągu indeksów).
(teraz już nie słowa, a ciągu indeksów). 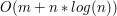 lub
lub 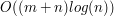 , gdzie
, gdzie  jest długością tego "zróżnicowanego" ciągu, czyli znacznie szybciej niż standardowy LCS. Do przemyślenia: co się stanie, gdy w tym drugim słowie każda z liter będzie występowała najwyżej
jest długością tego "zróżnicowanego" ciągu, czyli znacznie szybciej niż standardowy LCS. Do przemyślenia: co się stanie, gdy w tym drugim słowie każda z liter będzie występowała najwyżej  razy, gdzie
razy, gdzie 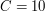 )? Czy potrafimy to rozwiązać w czasie
)? Czy potrafimy to rozwiązać w czasie 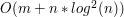 ?
?


