Właściwy algorytm
Tworzymy sobie listę warstw (czyli np. wektor wektorów liczb) i będziemy ją uzupełniać podobnie jak w naszym dynamiku.
Niech  będzie (coraz to kolejnym) elementem ciągu. Szukamy, binary searchem, największego takiego
będzie (coraz to kolejnym) elementem ciągu. Szukamy, binary searchem, największego takiego  , żeby
, żeby  mógł przedłużyć podciąg o długości
mógł przedłużyć podciąg o długości  . Czyli warstwy o jak największym numerze
. Czyli warstwy o jak największym numerze  takiej, żeby istniał w niej element mniejszy od
takiej, żeby istniał w niej element mniejszy od  . Jeśli dodatkowo postaramy się, żeby elementy w warstwach były posortowane malejąco, to wystarczy patrzeć tylko na "ogony" tych warstw/wektorów (ostatnie elementy). Zatem problem sprowadza się do znalezienia największej liczby mniejszej od zadanego
. Jeśli dodatkowo postaramy się, żeby elementy w warstwach były posortowane malejąco, to wystarczy patrzeć tylko na "ogony" tych warstw/wektorów (ostatnie elementy). Zatem problem sprowadza się do znalezienia największej liczby mniejszej od zadanego  , co już potrafimy (powinniśmy potrafić?) zrobić...
, co już potrafimy (powinniśmy potrafić?) zrobić...
Co dalej? Skoro znaleźliśmy takie  , to znaczy, że
, to znaczy, że  przedłuża podciąg rosnący o długości
przedłuża podciąg rosnący o długości  i żadnego dłuższego. Czyli musimy wrzucić element
i żadnego dłuższego. Czyli musimy wrzucić element  do warstwy/listy następnej,
do warstwy/listy następnej, 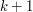 -szej. Oczywiście, będzie on tam najmniejszy (gdyby istniał mniejszy, to
-szej. Oczywiście, będzie on tam najmniejszy (gdyby istniał mniejszy, to  znalazłby się w którejś z następnych warstw) czyli wędruje po prostu na koniec tej listy/wektora.
znalazłby się w którejś z następnych warstw) czyli wędruje po prostu na koniec tej listy/wektora.
Koniec algorytmu! Aha, tylko co należy wypisać? Otóż LAS tego ciągu będzie długości takiej jak numer najdalszej, niepustej warstwy (bo tam będą siedziały elementy kończące najdłuższe podciągi rosnące). A ponieważ warstwy uzupełniają nam się po kolei, czyli nie będzie "dziur", zwracamy po prostu ich ilość.
Ważne w tym algorytmie jest to, że jest online! Czasem może nam się to przydać... Natomiast jego złożoność szacujemy przez  razy czas wykonania binary-searcha, czyli
razy czas wykonania binary-searcha, czyli 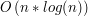 .
.
Oto algorytm w pseudokodzie:
vector<int> Layers[n];
int LongestEver = 0, Index;
for (int i=0; i<n; i += 1)
scanf(A);
Index = lower_bound(Layers.back, A);
/*Czyli najmniejszy element większy od A (lub równy!).
Zadanie bojowe dla czytelników: jak zaimplementować powyższą linijkę?
można użyć stl-owego lower_bound, ale to trochę zabawy;
proponuję napisanie własnej funkcji.*/
Layers[Index].Push_Back(A);
LongestEver = max(LongestEver, Index);
/*tutaj bierzemy maksimum ze wszystkich numerów niepustych warstw*/
printf(LongestEver);
Przykład. Oto jak będzie wyglądała nasza struktura jeden krok przed zakończeniem działania algorytmu dla ciągu: 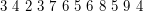 .
.
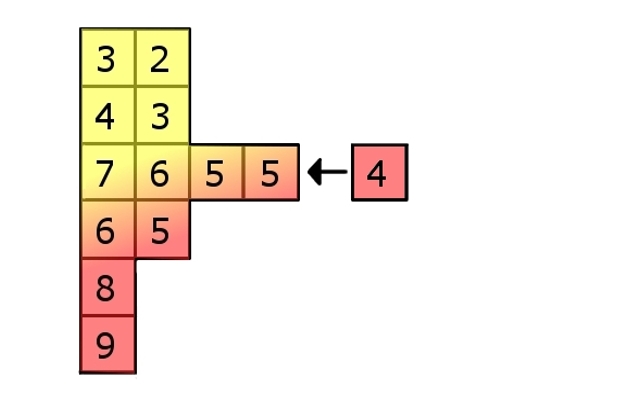
Skoro już umiemy liczyć długość takiego podciągu, zastanówmy się nad modyfikacją tego algorytmu umożliwiającą nam wypisanie go. Otóż przy każdym elemencie możemy pamiętać lokalizację poprzedniego (a nie tylko jego wartość, bo niektóre mogą być równe i sama wartość nic nam nie powie!). Czyli zamiast wrzucać do list elementy, wrzucamy pary: [wartość, indeks na liście poprzedniego elementu]. Wtedy idąc "od końca" (od dowolnego elementu z ostatniej warstwy), możemy odtworzyć cały ciąg.
Jeśli jednak zależy nam na pamięci albo pewnych własnościach tych LAS-ów (jako że może być ich kilka, a zostaniemy zapytani o jakiś specyficzny), musimy to zrobić inaczej. Najprościej nie modyfikować w ogóle struktury, tylko,, idąc "od tyłu", zachłannie wybierać pasujące nam elementy. Ale uwaga, pułapka! Otóż nie możemy jako poprzednika wziąć dowolnego elementu z warstwy poprzedniej, bo mógł zostać dodany później.
Rozważmy przykład:
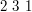
Wtedy w kolejnych warstwach będą:
warstwa 1: 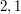
warstwa 2: 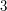 .
.
Po wybraniu elementu 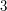 kusi, żeby wziąć
kusi, żeby wziąć  . Ale
. Ale 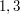 nie tworzą podciągu!
nie tworzą podciągu!
Najprostszą metodą jest, mając ustalony element  w warstwie
w warstwie 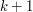 , wybrać z warstwy o numerze
, wybrać z warstwy o numerze  największy mniejszy od tego elementu. Czemu to jest dobrze? Bo wiemy (a przynajmniej jesteśmy przekonani) że nasz algorytm jest poprawny, czyli istnieje taki element w warstwie
największy mniejszy od tego elementu. Czemu to jest dobrze? Bo wiemy (a przynajmniej jesteśmy przekonani) że nasz algorytm jest poprawny, czyli istnieje taki element w warstwie  -tej, że można go przedłużyć elementem
-tej, że można go przedłużyć elementem  . Ale skoro elementy są posortowane nierosnąco po wartości i rosnąco po indeksie, to
. Ale skoro elementy są posortowane nierosnąco po wartości i rosnąco po indeksie, to  również przedłuży podciąg kończący się większym elementem, bo ten ma jednocześnie mniejszy indeks.
również przedłuży podciąg kończący się większym elementem, bo ten ma jednocześnie mniejszy indeks.
Zobaczmy, jak to wygląda na naszym rysunku: element '7' został dodany do trzeciej warstwy "z powodu" elementu '3' (czyli '3' była w drugiej warstwie, kiedy do trzeciej dopisaliśmy '7'). Ale '7' tym bardziej przedłuża podciąg kończący się na '4', bo '4' (będąc wcześniej w warstwie) ma mniejszy indeks.
Trochę matematyki
Rozważmy takie zadanie: Dany jest ciąg liczb o długości większej od 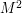 . Pokazać, że istnieje w nim podciąg monotoniczny o długości większej od
. Pokazać, że istnieje w nim podciąg monotoniczny o długości większej od 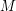 . Dowód korzystający z algorytmu: po odpaleniu go dla tego ciągu podzielimy jego elementy na warstwy. Gdyby było ich więcej niż
. Dowód korzystający z algorytmu: po odpaleniu go dla tego ciągu podzielimy jego elementy na warstwy. Gdyby było ich więcej niż 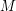 , to istniałby podciąg rosnący o takiej długości. Jeśli nie, to w którejś warstwie musiałoby być ponad
, to istniałby podciąg rosnący o takiej długości. Jeśli nie, to w którejś warstwie musiałoby być ponad 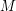 elementów. Ale wiemy, że w obrębie jednej warstwy elementy tworzą ciąg nierosnący, czyli też monotoniczny - koniec dowodu.
elementów. Ale wiemy, że w obrębie jednej warstwy elementy tworzą ciąg nierosnący, czyli też monotoniczny - koniec dowodu.
Taką samą argumentację można użyć do dowodu faktu: W każdym nieskończonym ciągu jest nieskończony podciąg monotoniczny (dla bardzo wtajemniczonych: dowodzi to błyskawicznie twierdzenia Bolzano-Weierstrassa. Fajnie, nie?...)
Zastanówmy się teraz nad pewnymi wariacjami problemu szukania LAS-u.




 będzie (coraz to kolejnym) elementem ciągu. Szukamy, binary searchem, największego takiego
będzie (coraz to kolejnym) elementem ciągu. Szukamy, binary searchem, największego takiego  , żeby
, żeby 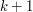 -szej. Oczywiście, będzie on tam najmniejszy (gdyby istniał mniejszy, to
-szej. Oczywiście, będzie on tam najmniejszy (gdyby istniał mniejszy, to  razy czas wykonania binary-searcha, czyli
razy czas wykonania binary-searcha, czyli 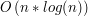 .
.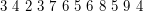 .
. 
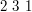
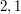
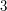 .
. . Ale
. Ale 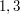 nie tworzą podciągu!
nie tworzą podciągu! 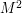 . Pokazać, że istnieje w nim podciąg monotoniczny o długości większej od
. Pokazać, że istnieje w nim podciąg monotoniczny o długości większej od 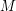 . Dowód korzystający z algorytmu: po odpaleniu go dla tego ciągu podzielimy jego elementy na warstwy. Gdyby było ich więcej niż
. Dowód korzystający z algorytmu: po odpaleniu go dla tego ciągu podzielimy jego elementy na warstwy. Gdyby było ich więcej niż 

