Wielka Przesmycka Reloaded 2011 - omówienie zadań
22.11.2011
D MrówkiTo zadanie okazało się być trudniejsze niż się spodziewaliśmy. Co prawda poprawne rozwiązanie wersji professional faktycznie wymaga kilku nietrywialnych spostrzeżeń, ale wersji basic wydawała nam się możliwa do rozwiązania przez zgadnięcie (dość prostego) warunku na istnienie rozwiązania. W zadaniu jesteśmy proszenie o sprawdzenie, czy krawędzie danego grafu nieskierowanego można zorientować w ten sposób, że otrzymany graf skierowany jest acykliczny, a w dodatku dla każdego wierzchołka
Lub inaczej ujmując kwestię, Zacznijmy od banalnej obserwacji: niespójne grafy na pewno nie mają interesującego uporządkowania. Dlaczego? Przede wszystkim skoro otrzymany graf skierowany ma być acykliczny, można go posortować topologicznie. Jeśli popatrzymy się następnie na dowolną spójną składową, ten z jej wierzchołków, który jest pierwszy (ostatni) topologicznie, nie ma żadnych wchodzących (wychodzących) krawędzi. Czyli jeśli jest więcej niż jedna składowa, muszą pojawić się przynajmniej dwa źródła i ujścia. Powyższa obserwacja jest dość jasną (co nie znaczy, że poprawną) wskazówką, że spójność grafu odgrywa kluczową rolę jeśli chodzi o istnienie interesującej orientacji. Skoro niespójne grafy nie posiadają takiej orientacji, to może powinniśmy przyjrzeć się takim, które są tylko odrobinę spójne? Czyli na przykład takim, w których istnieje most (krawędź, której usunięcie rozspaja graf). Niestety samo istnienie mostu jeszcze o niczym nie świadczy. Jeśli jednak wyobrazimy sobie sytuację podobną do tej z rysunku 6, dość łatwo przekonać się, że oznacza ona brak interesującej orientacji.
Rysunek 6: Obecnosc krawędzi Dlaczego? Cóż, jeśli w grafie niezależnie od ustalenia kierunków wszystkich krawędzi w składowej "po drugiej stronie" Mamy więc pierwszy pomysł na rozwiązanie. Dokładamy krawędź Okazuje się, że nie jest to takie trudne, ale niestety trzeba dobrze rozumieć jak działa przeszukiwanie w głąb w grafach nieskierowanych. Wiadomo, że używając go możemy podzielić wszystkie krawędzie na drzewowe i wsteczne. Każda (poza jedną użytą do skonstruowania początkowego cyklu prostego) krawędź wstecz definiuje nowe ucho (być może trywialne). Czytelnikowi pozostawiamy przyjemność dopowiedzenia szczegółów tego pomysłu (wymaga to tylko porządnego zrozumienia algorytmu sprawdzania dwuspójności). Niestety powyższy pomysł nie prowadzi jeszcze bezpośrednio do akceptowalnego rozwiązania. Co prawda dekompozycję na uszy można nie tak trudno skonstruować w czasie liniowym, ale konieczność przechowywania aktualnego liniowego porządku na wierzchołkach, a konkretnie jego aktualizacji, istotnie zwiększa złożoność. W takiej najbardziej naiwnej implementacji do Przyzwoitość wypada zdradzić, że takie orientowanie krawędzi grafu wcale nie jest tak bezużyteczne jak mogłoby się wydawać. Korzysta się z niego na przykład podczas sprawdzania planarności grafu. |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


 spełnione są dwa warunki:
spełnione są dwa warunki:
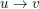 istnieje dla jakiegoś
istnieje dla jakiegoś 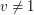 ,
,
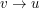 istnieje dla jakiegoś
istnieje dla jakiegoś 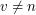 .
.
 jest jedynym źródłem, a
jest jedynym źródłem, a  jedynym ujściem. Takie zorientowanie będziemy nazywali interesującym. W wersji professional musimy nie tylko sprawdzić, czy takie uporządkowanie istnieje, ale także je podać.
jedynym ujściem. Takie zorientowanie będziemy nazywali interesującym. W wersji professional musimy nie tylko sprawdzić, czy takie uporządkowanie istnieje, ale także je podać.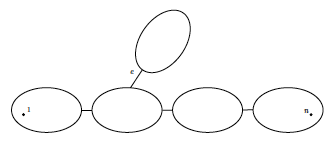
 uniemożliwia interesujaca orientację.
uniemożliwia interesujaca orientację.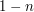 cały graf nie jest dwuspójny, interesująca orientacją nie jest możliwa.
cały graf nie jest dwuspójny, interesująca orientacją nie jest możliwa.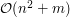 , ale... ale jak właściwie znaleźć rozkład na uszy?
, ale... ale jak właściwie znaleźć rozkład na uszy?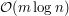 . Okazuje się, że istnieje jednak dość proste (gdy już się je zna) rozwiązanie liniowe. Wystarczy trochę uważniej przyjrzeć się jak dokładnie uaktualniamy porządek na wierzchołkach...
. Okazuje się, że istnieje jednak dość proste (gdy już się je zna) rozwiązanie liniowe. Wystarczy trochę uważniej przyjrzeć się jak dokładnie uaktualniamy porządek na wierzchołkach...

