A Mona Lisa
Na wejściu dostajemy tablicę 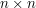 wypełnioną literami. Dla każdego spójnego fragmentu
wypełnioną literami. Dla każdego spójnego fragmentu 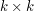 chcemy policzyć ile różnych liter można w nim znaleźć. Będziemy nazywali tą wartość jakością fragmentu.
chcemy policzyć ile różnych liter można w nim znaleźć. Będziemy nazywali tą wartość jakością fragmentu.
W wersji basic 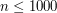 , ale
, ale 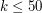 , co od razu nasuwa myśl, że wystarczyłoby rozwiązanie o złożoności
, co od razu nasuwa myśl, że wystarczyłoby rozwiązanie o złożoności 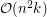 . Taki pierwszy najprostszy (a może nawet prymitywny) pomysł od razu daje algorytm o czasie działania
. Taki pierwszy najprostszy (a może nawet prymitywny) pomysł od razu daje algorytm o czasie działania 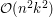 : dla każdego z
: dla każdego z 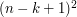 możliwych fragmentów przeglądamy wszystkie
możliwych fragmentów przeglądamy wszystkie 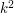 pola. Jak pozbyć się tego jednego
pola. Jak pozbyć się tego jednego  z czasu działania? Wystarczy tylko zauważyć, że dla sąsiednich fragmentów zdecydowana większość przeglądanych pól będzie dokładnie taka sama. Zakładając, że policzyliśmy ile jest pól każdego koloru w danym fragmencie, wyznaczenie takich statystyk dla fragmentu przesuniętego o jeden w pionie lub poziomie wymaga tylko dodania i odjęcia jednego rzędu lub kolumny. Taką operację możemy łatwo wykonać w czasie
z czasu działania? Wystarczy tylko zauważyć, że dla sąsiednich fragmentów zdecydowana większość przeglądanych pól będzie dokładnie taka sama. Zakładając, że policzyliśmy ile jest pól każdego koloru w danym fragmencie, wyznaczenie takich statystyk dla fragmentu przesuniętego o jeden w pionie lub poziomie wymaga tylko dodania i odjęcia jednego rzędu lub kolumny. Taką operację możemy łatwo wykonać w czasie 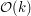 . Podczas wyznaczania statystyk dla kolejnego fragmentu możemy także łatwo uaktualniać liczbę kolorów, które występują przynajmniej raz, a więc uzyskujemy rozwiązanie całego problemu w wersji basic.
. Podczas wyznaczania statystyk dla kolejnego fragmentu możemy także łatwo uaktualniać liczbę kolorów, które występują przynajmniej raz, a więc uzyskujemy rozwiązanie całego problemu w wersji basic.
W wersji professional wiemy tylko, że 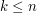 . Co samo w sobie nie jest szczególnie interesującą informacją... Naszym celem będzie uzyskanie rozwiązania o złożoności
. Co samo w sobie nie jest szczególnie interesującą informacją... Naszym celem będzie uzyskanie rozwiązania o złożoności 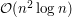 . Idea jest dość prosta: będziemy przetwarzali jednocześnie wszystkie fragmenty rozpoczynające się w tym samym wierszu. Przyjrzyjmy się bliżej jak wygląda sytuacja dla takich fragmentów. Każdy kolor (dla ustalenia uwagi: zielony) występujący w jednym z
. Idea jest dość prosta: będziemy przetwarzali jednocześnie wszystkie fragmenty rozpoczynające się w tym samym wierszu. Przyjrzyjmy się bliżej jak wygląda sytuacja dla takich fragmentów. Każdy kolor (dla ustalenia uwagi: zielony) występujący w jednym z  kolejnych wierszy powoduje zwiększenie jakości niektórych fragmentów o jeden. A dokładniej, jeśli mamy zielone pola w kolumnach
kolejnych wierszy powoduje zwiększenie jakości niektórych fragmentów o jeden. A dokładniej, jeśli mamy zielone pola w kolumnach 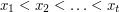 , gdzie
, gdzie 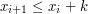 oraz
oraz 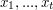 jest maksymalnym zbiorem kolumn o tej własności, to powinniśmy zwiększyć (o jeden) jakość wszystkich fragmentów zaczynających się w kolumnach od
jest maksymalnym zbiorem kolumn o tej własności, to powinniśmy zwiększyć (o jeden) jakość wszystkich fragmentów zaczynających się w kolumnach od 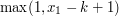 -tej do
-tej do 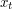 -tej, patrz rysunek 1.
-tej, patrz rysunek 1.
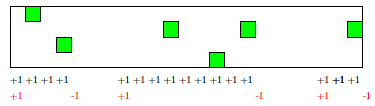
Rysunek 1: Zwiększanie jakości w wierszu ze względu na wystąpienia zielonego, 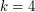 .
.
Pierwsza ważna obserwacja jest następująca: zamiast przechowywać te wszystkie 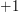 , lepiej dla każdej kolumny pamiętać dla ilu kolorów właśnie w tej kolumnie zaczyna pojawiać się
, lepiej dla każdej kolumny pamiętać dla ilu kolorów właśnie w tej kolumnie zaczyna pojawiać się 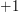 , a dla ilu kończy (lub, inaczej mówiąc, jaka jest suma po wszystkich kolorach czerwonych liczb z rysunku). Mając taką informację możemy łatwo wyznaczyć jakość każdego fragmentu zaczynającego się w danym wierszu idąc od lewej do prawej w czasie
, a dla ilu kończy (lub, inaczej mówiąc, jaka jest suma po wszystkich kolorach czerwonych liczb z rysunku). Mając taką informację możemy łatwo wyznaczyć jakość każdego fragmentu zaczynającego się w danym wierszu idąc od lewej do prawej w czasie 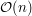 . Ale to oczywiście nie załatwia sprawy, musimy jeszcze umieć przejść do fragmentów zaczynających się o jeden wiersz niżej. Powiedzmy, że dana kolumna jest zielona jeśli występuje w niej przynajmniej jedno zielone pole. Jeżeli kolumna przestaje być zielona, być może musimy pozbyć się jakichś
. Ale to oczywiście nie załatwia sprawy, musimy jeszcze umieć przejść do fragmentów zaczynających się o jeden wiersz niżej. Powiedzmy, że dana kolumna jest zielona jeśli występuje w niej przynajmniej jedno zielone pole. Jeżeli kolumna przestaje być zielona, być może musimy pozbyć się jakichś 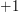 . Podobnie, jeżeli kolumna zaczyna być zielona, być może musimy dołożyć jakieś
. Podobnie, jeżeli kolumna zaczyna być zielona, być może musimy dołożyć jakieś 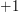 . Łatwo zauważyć, że zależy to tylko od pozycji poprzedniej i następnej zielonej kolumny! W szczególności, jeśli kolumna
. Łatwo zauważyć, że zależy to tylko od pozycji poprzedniej i następnej zielonej kolumny! W szczególności, jeśli kolumna  przestaje być zielona, ale odległość między poprzednią i następną nie przekracza
przestaje być zielona, ale odległość między poprzednią i następną nie przekracza  , nie musimy niczego zmieniać. W innych sytuacjach być może musimy dołożyć jeden blok złożony z
, nie musimy niczego zmieniać. W innych sytuacjach być może musimy dołożyć jeden blok złożony z 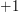 lub podzielić istniejący na dwa (być może zdegenerowane). Na rysunku~\rref{figure:quality_modify} można zobaczyć przykład tej drugiej sytuacji. W tym momencie widać dlaczego zamiast jawnie przechowywać wszystkie
lub podzielić istniejący na dwa (być może zdegenerowane). Na rysunku~\rref{figure:quality_modify} można zobaczyć przykład tej drugiej sytuacji. W tym momencie widać dlaczego zamiast jawnie przechowywać wszystkie 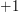 zdecydowaliśmy się pamiętać początki i końce bloków. Pozostaje tylko jeden problem: jak szybko znaleźć poprzednią/następną zieloną kolumnę? Wystarczy dla każdego koloru pamiętać w drzewie zrównoważonym (na przykład w set<int>) wszystkie aktywne kolumny...
zdecydowaliśmy się pamiętać początki i końce bloków. Pozostaje tylko jeden problem: jak szybko znaleźć poprzednią/następną zieloną kolumnę? Wystarczy dla każdego koloru pamiętać w drzewie zrównoważonym (na przykład w set<int>) wszystkie aktywne kolumny...
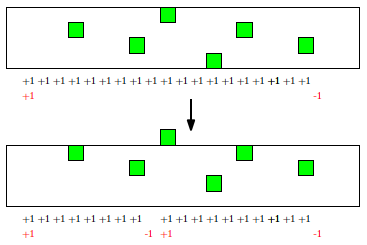
Rysunek 2: Po przesunięciu o jeden wiersz kolumna przestaje być zielona.
Oczywiście nie sposób przejść obojętnie obok pytania czy możliwe jest rozwiązanie liniowe (czyli w tym przypadku 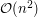 ). Co dość zaskakujące, jest to możliwe. Załóżmy, że
). Co dość zaskakujące, jest to możliwe. Załóżmy, że 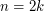 i podzielmy całą tablicę na 4 fragmenty
i podzielmy całą tablicę na 4 fragmenty  . Popatrzmy na zielone pola w lewym górnym kwadracie. Jeśli są tam pola
. Popatrzmy na zielone pola w lewym górnym kwadracie. Jeśli są tam pola  i
i  takie, że
takie, że  jest na prawo i poniżej
jest na prawo i poniżej  , to po chwili zastanowienia można dojść do wniosku, że
, to po chwili zastanowienia można dojść do wniosku, że  wcale nie jest nam potrzebne do szczęścia: każdy fragment, który zawiera
wcale nie jest nam potrzebne do szczęścia: każdy fragment, który zawiera  , zawiera także
, zawiera także  , patrz rysunek 2. Tak naprawdę wystarczy więc pozostawić w lewym górnym kwadracie tylko te pola, które nie są zdominowane przez żadne inne. Podobną operację możemy wykonać dla pozostałych kwadratów. Gdyby okazało się, że wszystkie zielone pola znajdują w lewym górnym kwadracie, takie uproszczenie wejścia dość łatwo pozwoliłoby nam na wyznaczenie wszystkich fragmentów w czasie proporcjonalnym do liczby zielonych pól, których jakość należy zwiększyć (wystarczy na przykład zauważyć, że po przesunięciu się o jeden wiersz w dół ich zbiór na pewno nie ulegnie zmniejszeniu).
, patrz rysunek 2. Tak naprawdę wystarczy więc pozostawić w lewym górnym kwadracie tylko te pola, które nie są zdominowane przez żadne inne. Podobną operację możemy wykonać dla pozostałych kwadratów. Gdyby okazało się, że wszystkie zielone pola znajdują w lewym górnym kwadracie, takie uproszczenie wejścia dość łatwo pozwoliłoby nam na wyznaczenie wszystkich fragmentów w czasie proporcjonalnym do liczby zielonych pól, których jakość należy zwiększyć (wystarczy na przykład zauważyć, że po przesunięciu się o jeden wiersz w dół ich zbiór na pewno nie ulegnie zmniejszeniu).
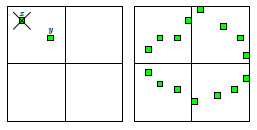
Rysunek 3: Tablica po usunieciu wszystkich niepotrzebnych zielonych pól.
Do rozwiązania pozostają dwie (nietrywialne) kwestie:
- sytuacja w jednym kwadracie jest prosta, ale fragment przecina cztery kwadraty jednocześnie...
- jak pozbyć się założenia, że
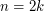 ?
?
Przyjemność zmierzenia się z nimi pozostawiamy Czytelnikowi.


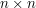 wypełnioną literami. Dla każdego spójnego fragmentu
wypełnioną literami. Dla każdego spójnego fragmentu 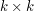 chcemy policzyć ile różnych liter można w nim znaleźć. Będziemy nazywali tą wartość jakością fragmentu.
chcemy policzyć ile różnych liter można w nim znaleźć. Będziemy nazywali tą wartość jakością fragmentu.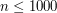 , ale
, ale 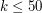 , co od razu nasuwa myśl, że wystarczyłoby rozwiązanie o złożoności
, co od razu nasuwa myśl, że wystarczyłoby rozwiązanie o złożoności 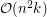 . Taki pierwszy najprostszy (a może nawet prymitywny) pomysł od razu daje algorytm o czasie działania
. Taki pierwszy najprostszy (a może nawet prymitywny) pomysł od razu daje algorytm o czasie działania 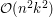 : dla każdego z
: dla każdego z 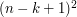 możliwych fragmentów przeglądamy wszystkie
możliwych fragmentów przeglądamy wszystkie 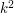 pola. Jak pozbyć się tego jednego
pola. Jak pozbyć się tego jednego  z czasu działania? Wystarczy tylko zauważyć, że dla sąsiednich fragmentów zdecydowana większość przeglądanych pól będzie dokładnie taka sama. Zakładając, że policzyliśmy ile jest pól każdego koloru w danym fragmencie, wyznaczenie takich statystyk dla fragmentu przesuniętego o jeden w pionie lub poziomie wymaga tylko dodania i odjęcia jednego rzędu lub kolumny. Taką operację możemy łatwo wykonać w czasie
z czasu działania? Wystarczy tylko zauważyć, że dla sąsiednich fragmentów zdecydowana większość przeglądanych pól będzie dokładnie taka sama. Zakładając, że policzyliśmy ile jest pól każdego koloru w danym fragmencie, wyznaczenie takich statystyk dla fragmentu przesuniętego o jeden w pionie lub poziomie wymaga tylko dodania i odjęcia jednego rzędu lub kolumny. Taką operację możemy łatwo wykonać w czasie 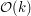 . Podczas wyznaczania statystyk dla kolejnego fragmentu możemy także łatwo uaktualniać liczbę kolorów, które występują przynajmniej raz, a więc uzyskujemy rozwiązanie całego problemu w wersji basic.
. Podczas wyznaczania statystyk dla kolejnego fragmentu możemy także łatwo uaktualniać liczbę kolorów, które występują przynajmniej raz, a więc uzyskujemy rozwiązanie całego problemu w wersji basic.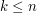 . Co samo w sobie nie jest szczególnie interesującą informacją... Naszym celem będzie uzyskanie rozwiązania o złożoności
. Co samo w sobie nie jest szczególnie interesującą informacją... Naszym celem będzie uzyskanie rozwiązania o złożoności 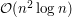 . Idea jest dość prosta: będziemy przetwarzali jednocześnie wszystkie fragmenty rozpoczynające się w tym samym wierszu. Przyjrzyjmy się bliżej jak wygląda sytuacja dla takich fragmentów. Każdy kolor (dla ustalenia uwagi: zielony) występujący w jednym z
. Idea jest dość prosta: będziemy przetwarzali jednocześnie wszystkie fragmenty rozpoczynające się w tym samym wierszu. Przyjrzyjmy się bliżej jak wygląda sytuacja dla takich fragmentów. Każdy kolor (dla ustalenia uwagi: zielony) występujący w jednym z 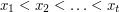 , gdzie
, gdzie 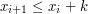 oraz
oraz 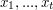 jest maksymalnym zbiorem kolumn o tej własności, to powinniśmy zwiększyć (o jeden) jakość wszystkich fragmentów zaczynających się w kolumnach od
jest maksymalnym zbiorem kolumn o tej własności, to powinniśmy zwiększyć (o jeden) jakość wszystkich fragmentów zaczynających się w kolumnach od 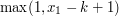 -tej do
-tej do 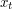 -tej, patrz rysunek 1.
-tej, patrz rysunek 1.
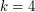 .
.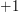 , lepiej dla każdej kolumny pamiętać dla ilu kolorów właśnie w tej kolumnie zaczyna pojawiać się
, lepiej dla każdej kolumny pamiętać dla ilu kolorów właśnie w tej kolumnie zaczyna pojawiać się 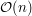 . Ale to oczywiście nie załatwia sprawy, musimy jeszcze umieć przejść do fragmentów zaczynających się o jeden wiersz niżej. Powiedzmy, że dana kolumna jest zielona jeśli występuje w niej przynajmniej jedno zielone pole. Jeżeli kolumna przestaje być zielona, być może musimy pozbyć się jakichś
. Ale to oczywiście nie załatwia sprawy, musimy jeszcze umieć przejść do fragmentów zaczynających się o jeden wiersz niżej. Powiedzmy, że dana kolumna jest zielona jeśli występuje w niej przynajmniej jedno zielone pole. Jeżeli kolumna przestaje być zielona, być może musimy pozbyć się jakichś  przestaje być zielona, ale odległość między poprzednią i następną nie przekracza
przestaje być zielona, ale odległość między poprzednią i następną nie przekracza 
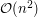 ). Co dość zaskakujące, jest to możliwe. Załóżmy, że
). Co dość zaskakujące, jest to możliwe. Załóżmy, że 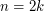 i podzielmy całą tablicę na 4 fragmenty
i podzielmy całą tablicę na 4 fragmenty 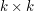 . Popatrzmy na zielone pola w lewym górnym kwadracie. Jeśli są tam pola
. Popatrzmy na zielone pola w lewym górnym kwadracie. Jeśli są tam pola  takie, że
takie, że 


