E Drużyna
Po usunięciu z treści profesora M. otrzymujemy dość krótkie sformułowanie: dla danych dwóch napisów  i
i  chcemy policzyć (modulo
chcemy policzyć (modulo 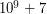 ) ile jest różnych napisów
) ile jest różnych napisów  , które są podciągami (niekoniecznie spójnymi)
, które są podciągami (niekoniecznie spójnymi)  , ale jednocześnie
, ale jednocześnie  jest podciągiem
jest podciągiem  . Limity wersji basic (
. Limity wersji basic (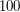 ) sugerują rozwiązanie sześcienne, a wersji professional (
) sugerują rozwiązanie sześcienne, a wersji professional (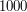 ) kwadratowe.
) kwadratowe.
Rozwiązywanie warto zacząć od uproszczonej wersji zadania, w której  jest pusty. Zacznijmy od prostej obserwacji: jeśli ktoś poda nam
jest pusty. Zacznijmy od prostej obserwacji: jeśli ktoś poda nam  , można bardzo łatwo sprawdzić czy jest on podciągiem
, można bardzo łatwo sprawdzić czy jest on podciągiem  . Wystarczy tylko znaleźć pierwsze wystąpienie
. Wystarczy tylko znaleźć pierwsze wystąpienie ![$ x[1] $](/files/tex/be0bfc068785699785e7ce2649aef514a0322872.png) w
w  , na prawo od niego wyszukać pierwsze wystąpienie
, na prawo od niego wyszukać pierwsze wystąpienie ![$ x[2] $](/files/tex/9d3fc050b6ea6cebf12a9fa57ed7040190aabd91.png) , i tak dalej... Oczywiście nie ma co liczyć na to, że ktoś poda nam chociaż jedno prawidłowe
, i tak dalej... Oczywiście nie ma co liczyć na to, że ktoś poda nam chociaż jedno prawidłowe  (bo właściwie po co miałby to robić?). Widać jednak, że warunek, który musimy sprawdzać, jest w pewnym sensie lokalny. A dokładniej, aby policzyć różne podciągi
(bo właściwie po co miałby to robić?). Widać jednak, że warunek, który musimy sprawdzać, jest w pewnym sensie lokalny. A dokładniej, aby policzyć różne podciągi  możemy wysumować po wszystkich literach
możemy wysumować po wszystkich literach  (występujących w
(występujących w  ) liczbę różnych podciągów sufiksu
) liczbę różnych podciągów sufiksu  zaczynającego się tuż za pierwszym wystąpieniem
zaczynającego się tuż za pierwszym wystąpieniem  ! Co od razu nasuwa proste rozwiązanie używające programowania dynamicznego, które działa w czasie
! Co od razu nasuwa proste rozwiązanie używające programowania dynamicznego, które działa w czasie 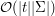 , gdzie
, gdzie 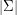 jest rozmiarem alfabetu. Dość łatwo zmniejszyć jego złożoność do
jest rozmiarem alfabetu. Dość łatwo zmniejszyć jego złożoność do 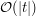 zauważając, że suma, którą liczymy dla
zauważając, że suma, którą liczymy dla  różni się co najwyżej dwoma składnikami od sumy, którą już policzyliśmy dla
różni się co najwyżej dwoma składnikami od sumy, którą już policzyliśmy dla ![$ t[2..|t|] $](/files/tex/fc754626eede57042259ed151be6c9da74bc38c0.png) (być może trzeba wykreślić jeden z nich i dodać nowy).
(być może trzeba wykreślić jeden z nich i dodać nowy).
No dobra, ale przecież  wcale nie musi być pusty (a właściwie to zgodnie z treścią zadania nigdy taki nie będzie, co sprawia, że powyższe rozumowanie może wydawać się lekko bezużyteczne). Na szczęście nawet w ogólnym przypadku możemy użyć bardzo podobnego pomysłu. Jeśli znamy pierwszą literą
wcale nie musi być pusty (a właściwie to zgodnie z treścią zadania nigdy taki nie będzie, co sprawia, że powyższe rozumowanie może wydawać się lekko bezużyteczne). Na szczęście nawet w ogólnym przypadku możemy użyć bardzo podobnego pomysłu. Jeśli znamy pierwszą literą  , to oczywiście najlepiej dopasować ją do pierwszego wystąpienia w
, to oczywiście najlepiej dopasować ją do pierwszego wystąpienia w  . Mamy dwie możliwe sytuacje:
. Mamy dwie możliwe sytuacje:
![$ x[1]=s[1] $](/files/tex/0cd0cc2c799d5e1d946e3c4ed2eabe6bb029dae6.png) , wtedy
, wtedy ![$ x[2..|x|] $](/files/tex/94a411a7be24382a32685f7a66d763de922db36c.png) musi zawierać
musi zawierać ![$ s[2..|s|] $](/files/tex/bd0c65e8ac696fe1af357fbeda530fffac4af08b.png) .
.
![$ x[1]\neq s[1] $](/files/tex/1f44b47c1d467d8139d5e27e3ebf48161c7678d6.png) , wtedy
, wtedy ![$ x[2..|x|] $](/files/tex/94a411a7be24382a32685f7a66d763de922db36c.png) musi zawierać całe
musi zawierać całe  .
.
Widać więc, że zgadnięcie ![$ x[1] $](/files/tex/be0bfc068785699785e7ce2649aef514a0322872.png) pozwoliłoby by nam zredukować oryginalny problem do podobnego, tyle że mniejszego. Zgadywać nie umiemy, ale możemy wysumować odpowiedzi po wszystkich możliwych
pozwoliłoby by nam zredukować oryginalny problem do podobnego, tyle że mniejszego. Zgadywać nie umiemy, ale możemy wysumować odpowiedzi po wszystkich możliwych ![$ x[1] $](/files/tex/be0bfc068785699785e7ce2649aef514a0322872.png) . Wszystkie pojawiające się problem mają taką samą strukturę:
. Wszystkie pojawiające się problem mają taką samą strukturę:  jest sufiksem oryginalnego
jest sufiksem oryginalnego  , a
, a  oryginalnego
oryginalnego  . A więc znowu możemy użyć programowania dynamicznego, tym razem uzyskując rozwiązanie działające w czasie
. A więc znowu możemy użyć programowania dynamicznego, tym razem uzyskując rozwiązanie działające w czasie 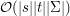 , co w zupełności wystarczało do pokonania wersji basic. W zależności od szczegółów implementacji dla wersji professional taki pomysł kończył się komunikatem Accepted lub Time Limit Exceeded. Naszą intencją było tak naprawdę zachęcenie Was do zaimplementowania rozwiązania o złożoności
, co w zupełności wystarczało do pokonania wersji basic. W zależności od szczegółów implementacji dla wersji professional taki pomysł kończył się komunikatem Accepted lub Time Limit Exceeded. Naszą intencją było tak naprawdę zachęcenie Was do zaimplementowania rozwiązania o złożoności 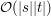 używając podobnego pomysłu jak ten użyty do zmniejszenia czasu działania w prostszej wersji. Można zauważyć, że sumy liczone dla kolejnych podproblemów są tak naprawdę bardzo podobne do siebie, a w związku z tym zamiast liczyć je za każdym razem od początku, możemy uaktualnić poprzednio wyznaczoną wartość. Szczegóły pozostawiamy domyślności Czytelnika.
używając podobnego pomysłu jak ten użyty do zmniejszenia czasu działania w prostszej wersji. Można zauważyć, że sumy liczone dla kolejnych podproblemów są tak naprawdę bardzo podobne do siebie, a w związku z tym zamiast liczyć je za każdym razem od początku, możemy uaktualnić poprzednio wyznaczoną wartość. Szczegóły pozostawiamy domyślności Czytelnika.


 i
i  chcemy policzyć (modulo
chcemy policzyć (modulo 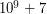 ) ile jest różnych napisów
) ile jest różnych napisów  , które są podciągami (niekoniecznie spójnymi)
, które są podciągami (niekoniecznie spójnymi) 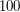 ) sugerują rozwiązanie sześcienne, a wersji professional (
) sugerują rozwiązanie sześcienne, a wersji professional (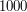 ) kwadratowe.
) kwadratowe.![$ x[1] $](/files/tex/be0bfc068785699785e7ce2649aef514a0322872.png) w
w ![$ x[2] $](/files/tex/9d3fc050b6ea6cebf12a9fa57ed7040190aabd91.png) , i tak dalej... Oczywiście nie ma co liczyć na to, że ktoś poda nam chociaż jedno prawidłowe
, i tak dalej... Oczywiście nie ma co liczyć na to, że ktoś poda nam chociaż jedno prawidłowe  (występujących w
(występujących w 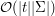 , gdzie
, gdzie 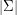 jest rozmiarem alfabetu. Dość łatwo zmniejszyć jego złożoność do
jest rozmiarem alfabetu. Dość łatwo zmniejszyć jego złożoność do 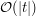 zauważając, że suma, którą liczymy dla
zauważając, że suma, którą liczymy dla ![$ t[2..|t|] $](/files/tex/fc754626eede57042259ed151be6c9da74bc38c0.png) (być może trzeba wykreślić jeden z nich i dodać nowy).
(być może trzeba wykreślić jeden z nich i dodać nowy).![$ x[1]=s[1] $](/files/tex/0cd0cc2c799d5e1d946e3c4ed2eabe6bb029dae6.png) , wtedy
, wtedy ![$ x[2..|x|] $](/files/tex/94a411a7be24382a32685f7a66d763de922db36c.png) musi zawierać
musi zawierać ![$ s[2..|s|] $](/files/tex/bd0c65e8ac696fe1af357fbeda530fffac4af08b.png) .
.
![$ x[1]\neq s[1] $](/files/tex/1f44b47c1d467d8139d5e27e3ebf48161c7678d6.png) , wtedy
, wtedy 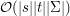 , co w zupełności wystarczało do pokonania wersji basic. W zależności od szczegółów implementacji dla wersji professional taki pomysł kończył się komunikatem Accepted lub Time Limit Exceeded. Naszą intencją było tak naprawdę zachęcenie Was do zaimplementowania rozwiązania o złożoności
, co w zupełności wystarczało do pokonania wersji basic. W zależności od szczegółów implementacji dla wersji professional taki pomysł kończył się komunikatem Accepted lub Time Limit Exceeded. Naszą intencją było tak naprawdę zachęcenie Was do zaimplementowania rozwiązania o złożoności 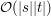 używając podobnego pomysłu jak ten użyty do zmniejszenia czasu działania w prostszej wersji. Można zauważyć, że sumy liczone dla kolejnych podproblemów są tak naprawdę bardzo podobne do siebie, a w związku z tym zamiast liczyć je za każdym razem od początku, możemy uaktualnić poprzednio wyznaczoną wartość. Szczegóły pozostawiamy domyślności Czytelnika.
używając podobnego pomysłu jak ten użyty do zmniejszenia czasu działania w prostszej wersji. Można zauważyć, że sumy liczone dla kolejnych podproblemów są tak naprawdę bardzo podobne do siebie, a w związku z tym zamiast liczyć je za każdym razem od początku, możemy uaktualnić poprzednio wyznaczoną wartość. Szczegóły pozostawiamy domyślności Czytelnika.

