C Połącz kropki
To zadanie miało być typowym "zamulaczem", którego nie może zabraknąć w żadnym szanującym się zestawie. Można powiedzieć, że świetnie sprawdziło się w tej roli: nikt nie próbował go rozwiązać, choć być może głównie ze względu na długą treść (i to w dodatku o Jasiu).
Dla danego drzewa  definiujemy jego deck jako (multi)zbiór lasów powstałych przez usunięcie dokładnie jednego wierzchołka. W wersji basic naszym zadaniem jest sprawdzenie, czy podany na wejściu multizbiór
definiujemy jego deck jako (multi)zbiór lasów powstałych przez usunięcie dokładnie jednego wierzchołka. W wersji basic naszym zadaniem jest sprawdzenie, czy podany na wejściu multizbiór  lasów jest deckiem pewnego drzewa
lasów jest deckiem pewnego drzewa  . Co więcej,
. Co więcej, 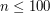 , a więc jasno widać, że będziemy mogli poszaleć ze złożonością rozwiązania. Pierwsza przydatna obserwacja jest następująca: w decku
, a więc jasno widać, że będziemy mogli poszaleć ze złożonością rozwiązania. Pierwsza przydatna obserwacja jest następująca: w decku  na pewno znajduje się las składający się z tylko jednego drzewa. Dlaczego? Każde drzewo ma przynajmniej jeden liść, a usunięcie liście nie rozspaja drzewa. W drugą stronę, każdy las składający się z tylko jednego drzewa musiał powstać przez usunięcie liścia. Nasuwa to dość prosty pomysł na rozwiązanie: wybieramy z decku las składający się z jednego drzewa (jeśli takiego nie ma od razy wypisujemy NIE), a następnie próbujemy "doczepić" do niego jeden dodatkowy wierzchołek na wszystkie
na pewno znajduje się las składający się z tylko jednego drzewa. Dlaczego? Każde drzewo ma przynajmniej jeden liść, a usunięcie liście nie rozspaja drzewa. W drugą stronę, każdy las składający się z tylko jednego drzewa musiał powstać przez usunięcie liścia. Nasuwa to dość prosty pomysł na rozwiązanie: wybieramy z decku las składający się z jednego drzewa (jeśli takiego nie ma od razy wypisujemy NIE), a następnie próbujemy "doczepić" do niego jeden dodatkowy wierzchołek na wszystkie 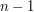 sposoby. Trzeba by tylko sprytnie sprawdzić czy po takim doczepieniu dostajemy
sposoby. Trzeba by tylko sprytnie sprawdzić czy po takim doczepieniu dostajemy  , które ma taki sam deck jak ten podany na wejściu. Jak to zrobić? Najprościej skonstruować (multi)zbiór lasów powstałych przez usunięcie dokładnie jednego wierzchołka i sprawdzić czy jest taki sam... W tym momencie już jasno widać, że w tym zadaniu nie obejdziemy się bez sprytnego sprawdzania czy dwa drzewa są takie same. Co prawda taki problem jest dość trudny dla dowolnych grafów, ale dla drzew istnieje dość proste (choć wcale nie oczywiste) rozwiązanie liniowe. Co więcej, można go użyć aby dla każdego drzewa wyznaczyć jego unikalny identyfikator (liczbę naturalną nie przekraczającą sumarycznej liczby wierzchołków) o takiej własności, że identyfikatory dwóch drzew są takie same wtedy i tylko wtedy gdy drzewa są izomorficzne. Mając te wszystkie identyfikatory możemy łatwo sprawdzić czy dane dwa decki są takie same: wystarczy posortować identyfikatory drzew w każdym lesie, a następnie uporządkować leksykograficznie otrzymane krotki. Jaki będzie czas działania całego rozwiązania? Doczepiając liść na
, które ma taki sam deck jak ten podany na wejściu. Jak to zrobić? Najprościej skonstruować (multi)zbiór lasów powstałych przez usunięcie dokładnie jednego wierzchołka i sprawdzić czy jest taki sam... W tym momencie już jasno widać, że w tym zadaniu nie obejdziemy się bez sprytnego sprawdzania czy dwa drzewa są takie same. Co prawda taki problem jest dość trudny dla dowolnych grafów, ale dla drzew istnieje dość proste (choć wcale nie oczywiste) rozwiązanie liniowe. Co więcej, można go użyć aby dla każdego drzewa wyznaczyć jego unikalny identyfikator (liczbę naturalną nie przekraczającą sumarycznej liczby wierzchołków) o takiej własności, że identyfikatory dwóch drzew są takie same wtedy i tylko wtedy gdy drzewa są izomorficzne. Mając te wszystkie identyfikatory możemy łatwo sprawdzić czy dane dwa decki są takie same: wystarczy posortować identyfikatory drzew w każdym lesie, a następnie uporządkować leksykograficznie otrzymane krotki. Jaki będzie czas działania całego rozwiązania? Doczepiając liść na 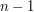 sposobów, a następnie usuwając wierzchołek na wszystkie
sposobów, a następnie usuwając wierzchołek na wszystkie  możliwe sposoby, dostajemy
możliwe sposoby, dostajemy 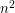 drzew (każde na
drzew (każde na 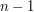 wierzchołkach). Jeśli użyjemy liniowego algorytmu wyznaczającego ich identyfikatory, cała złożoność to
wierzchołkach). Jeśli użyjemy liniowego algorytmu wyznaczającego ich identyfikatory, cała złożoność to 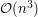 . Limity czasowe były dobrane tak, aby wystarczyło wyznaczyć identyfikatory w czasie liniowo-logarytmicznym, a więc w sumarycznej złożoności
. Limity czasowe były dobrane tak, aby wystarczyło wyznaczyć identyfikatory w czasie liniowo-logarytmicznym, a więc w sumarycznej złożoności 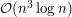 .
.
Sytuacja w wersji professional na pierwszy rzut oka wydaje się podobna. Tym razem dostajemy tylko dwa lasy powstałe przez usunięcie z  dwóch różnych wierzchołków, naszym zadaniem jest (tak jak poprzednio) odtworzenie drzewa. Jeśli jeden z tych lasów jest drzewem, możemy użyć pomysłu z wersji basic. Ale oczywiście wcale tak nie musi być...
dwóch różnych wierzchołków, naszym zadaniem jest (tak jak poprzednio) odtworzenie drzewa. Jeśli jeden z tych lasów jest drzewem, możemy użyć pomysłu z wersji basic. Ale oczywiście wcale tak nie musi być...
Pierwszy pomysł mógłby polegać na zgadnięciu sąsiadów usuniętych wierzchołków. W tym celu wystarczy wybrać dokładnie jeden wierzchołek w każdym drzewie (z obydwu lasów). Niestety tych drzew może być całkiem sporo i taka metoda raczej nie zakończy się niczym więcej niż bólem głowy. Możemy jednak popatrzeć na to zgadywanie w trochę inny sposób. Niech pierwszy las powstaje przez usunięcie  z
z  , a drugie przez usunięcie
, a drugie przez usunięcie  z
z  . Informacja o sąsiadach
. Informacja o sąsiadach  (
( ) jest w pewnym sensie zakodowana w
) jest w pewnym sensie zakodowana w 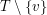 (
(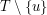 ), tylko jak ją wydostać? Wyobraźmy sobie, że wiemy który wierzchołek w
), tylko jak ją wydostać? Wyobraźmy sobie, że wiemy który wierzchołek w 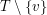 (
(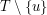 ) odpowiada
) odpowiada  (
( ). Wtedy po ich usunięciu (z obydwu lasów) musimy otrzymać dwa izomorficzne zbiory drzew, patrz rysunek 4.
). Wtedy po ich usunięciu (z obydwu lasów) musimy otrzymać dwa izomorficzne zbiory drzew, patrz rysunek 4.
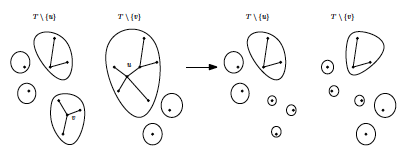
Rysunek 4: Lasy po usunięciu  i
i  .
.
Mamy więc pierwszy pomysł na rozwiązanie: spróbuj usunąć po jednym wierzchołku z każdego lasu tak, aby otrzymać izomorficzne lasy. Pojawiają się jednak (przynajmniej) dwa problemy:
- mamy
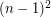 możliwości usunięcia po jednym wierzchołku z każdego lasu, dla każdej z nich musimy sprawdzić izomorfizm drzew, a więc cała złożoność to
możliwości usunięcia po jednym wierzchołku z każdego lasu, dla każdej z nich musimy sprawdzić izomorfizm drzew, a więc cała złożoność to 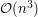 ... trochę sporo.
... trochę sporo. - jasne jest, że izomorfizm lasów jest warunkiem koniecznym, ale czy także wystarczającym? A więc, inaczej mówiąc, czy przypadkiem takie rozwiązanie jest poprawne?
Na szczęście okazuje się, że poradzenie sobie z tym pierwszym problemem może chwilę poczekać, ponieważ... takie rozwiązanie wcale nie jest poprawne. Okazuje się, że porządek drzew w otrzymanych lasach jest (trochę) istotny. A dokładniej, niech 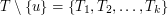 i załóżmy, że usuwamy wierzchołek
i załóżmy, że usuwamy wierzchołek 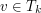 otrzymując
otrzymując 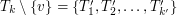 . Dodatkowo załóżmy, że
. Dodatkowo załóżmy, że  było połączone z wierzchołkiem z
było połączone z wierzchołkiem z 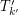 . Wtedy {\bf sygnaturą} nazywamy trójkę składającą się z
. Wtedy {\bf sygnaturą} nazywamy trójkę składającą się z 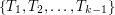 ,
, 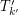 i
i 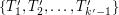 , patrz rysunek 5. Podobnie definiujemy sygnaturę dla lasu otrzymanego z
, patrz rysunek 5. Podobnie definiujemy sygnaturę dla lasu otrzymanego z 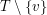 , przy czym tutaj pierwszy i trzeci element krotki są ze sobą zamienione. Można udowodnić, że sygnatury
, przy czym tutaj pierwszy i trzeci element krotki są ze sobą zamienione. Można udowodnić, że sygnatury 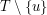 i
i 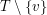 są takie same wtedy i tylko wtedy gdy dane wejściowe faktycznie odpowiadają pewnemu drzewu
są takie same wtedy i tylko wtedy gdy dane wejściowe faktycznie odpowiadają pewnemu drzewu  . Pozostaje jednak jeden problem: założyliśmy, że znamy drzewa połączone z
. Pozostaje jednak jeden problem: założyliśmy, że znamy drzewa połączone z  i
i  . Na szczęście nasz pomysł i tak nie będzie jakiś szczególnie szybki: usuwamy na wszystkie możliwe sposoby (jest ich
. Na szczęście nasz pomysł i tak nie będzie jakiś szczególnie szybki: usuwamy na wszystkie możliwe sposoby (jest ich 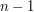 ) po jednym wierzchołku z każdego lasu. Równie dobrze możemy od razu zgadnąć po jednym sąsiedzie każdego z nich (zwiększy to ilość kombinacji w każdym lesie do
) po jednym wierzchołku z każdego lasu. Równie dobrze możemy od razu zgadnąć po jednym sąsiedzie każdego z nich (zwiększy to ilość kombinacji w każdym lesie do 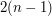 , czyli tylko dwukrotnie).
, czyli tylko dwukrotnie).
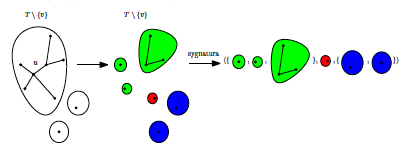
Rysunek 5: Jedna z sygnatur otrzymanych na podstawie 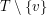 .
.
No dobrze, czyli mamy 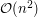 podproblemów, w każdym z nich musimy sprawdzić izomorfizm drzew. Czyli sumaryczny czas działania to, przy najlepszych chęciach,
podproblemów, w każdym z nich musimy sprawdzić izomorfizm drzew. Czyli sumaryczny czas działania to, przy najlepszych chęciach, 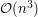 . A więc nawet przy poprawnej implementacji i tak dostaniemy Time Limit Exceeded. Jak sobie z tym poradzić? Kluczowe jest następujące spostrzeżenie: to co tak naprawdę robimy, to sprawdzenie czy dwa zbiory mają wspólny element. Zamiast zgadywać po jednym elemencie z każdego z nich i sprawdzać czy jest to tak naprawdę ten sam element, o wiele lepszym pomysłem jest wygenerowanie i zapamiętanie pierwszego zbioru, a następnie przeglądanie drugiego. Dla każdego z jego elementów sprawdzamy czy był on wcześniej zapamiętany. Przy odrobinie staranności (i po zauważeniu, że zapomnieliśmy o jednym szczególnym przypadku) daje to rozwiązanie działające w czasie
. A więc nawet przy poprawnej implementacji i tak dostaniemy Time Limit Exceeded. Jak sobie z tym poradzić? Kluczowe jest następujące spostrzeżenie: to co tak naprawdę robimy, to sprawdzenie czy dwa zbiory mają wspólny element. Zamiast zgadywać po jednym elemencie z każdego z nich i sprawdzać czy jest to tak naprawdę ten sam element, o wiele lepszym pomysłem jest wygenerowanie i zapamiętanie pierwszego zbioru, a następnie przeglądanie drugiego. Dla każdego z jego elementów sprawdzamy czy był on wcześniej zapamiętany. Przy odrobinie staranności (i po zauważeniu, że zapomnieliśmy o jednym szczególnym przypadku) daje to rozwiązanie działające w czasie 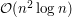 .
.


 definiujemy jego deck jako (multi)zbiór lasów powstałych przez usunięcie dokładnie jednego wierzchołka. W wersji basic naszym zadaniem jest sprawdzenie, czy podany na wejściu multizbiór
definiujemy jego deck jako (multi)zbiór lasów powstałych przez usunięcie dokładnie jednego wierzchołka. W wersji basic naszym zadaniem jest sprawdzenie, czy podany na wejściu multizbiór  lasów jest deckiem pewnego drzewa
lasów jest deckiem pewnego drzewa 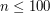 , a więc jasno widać, że będziemy mogli poszaleć ze złożonością rozwiązania. Pierwsza przydatna obserwacja jest następująca: w decku
, a więc jasno widać, że będziemy mogli poszaleć ze złożonością rozwiązania. Pierwsza przydatna obserwacja jest następująca: w decku 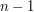 sposoby. Trzeba by tylko sprytnie sprawdzić czy po takim doczepieniu dostajemy
sposoby. Trzeba by tylko sprytnie sprawdzić czy po takim doczepieniu dostajemy 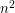 drzew (każde na
drzew (każde na 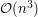 . Limity czasowe były dobrane tak, aby wystarczyło wyznaczyć identyfikatory w czasie liniowo-logarytmicznym, a więc w sumarycznej złożoności
. Limity czasowe były dobrane tak, aby wystarczyło wyznaczyć identyfikatory w czasie liniowo-logarytmicznym, a więc w sumarycznej złożoności 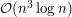 .
. z
z  z
z 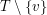 (
(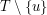 ), tylko jak ją wydostać? Wyobraźmy sobie, że wiemy który wierzchołek w
), tylko jak ją wydostać? Wyobraźmy sobie, że wiemy który wierzchołek w 
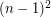 możliwości usunięcia po jednym wierzchołku z każdego lasu, dla każdej z nich musimy sprawdzić izomorfizm drzew, a więc cała złożoność to
możliwości usunięcia po jednym wierzchołku z każdego lasu, dla każdej z nich musimy sprawdzić izomorfizm drzew, a więc cała złożoność to 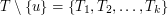 i załóżmy, że usuwamy wierzchołek
i załóżmy, że usuwamy wierzchołek 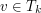 otrzymując
otrzymując 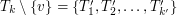 . Dodatkowo załóżmy, że
. Dodatkowo załóżmy, że 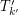 . Wtedy {\bf sygnaturą} nazywamy trójkę składającą się z
. Wtedy {\bf sygnaturą} nazywamy trójkę składającą się z 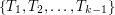 ,
, 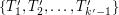 , patrz rysunek 5. Podobnie definiujemy sygnaturę dla lasu otrzymanego z
, patrz rysunek 5. Podobnie definiujemy sygnaturę dla lasu otrzymanego z 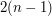 , czyli tylko dwukrotnie).
, czyli tylko dwukrotnie).
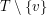 .
.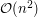 podproblemów, w każdym z nich musimy sprawdzić izomorfizm drzew. Czyli sumaryczny czas działania to, przy najlepszych chęciach,
podproblemów, w każdym z nich musimy sprawdzić izomorfizm drzew. Czyli sumaryczny czas działania to, przy najlepszych chęciach, 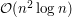 .
.


