B Nobel
W tym zadaniu jesteśmy proszeni o przedstawienie danego  jako sumy k {\bf różnych} liczb naturalnych z przedziału
jako sumy k {\bf różnych} liczb naturalnych z przedziału ![$ [1,n] $](/files/tex/22cbb292a9943b8e56b2b467a0dddbe0f5afb786.png) . Zacznijmy od dwóch prostych spostrzeżeń:
. Zacznijmy od dwóch prostych spostrzeżeń:
- najmniejszą liczbą, którą można w ten sposób przedstawić, na pewno jest
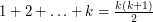 ,
, - największą liczbą, którą można w ten sposób przedstawić, na pewno jest
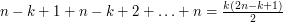 .
.
Okazuje się, że wszystkie liczby pomiędzy 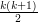 a
a 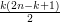 da się przedstawić jako sumę
da się przedstawić jako sumę  różnych liczb z przedziału
różnych liczb z przedziału ![$ [1,n] $](/files/tex/22cbb292a9943b8e56b2b467a0dddbe0f5afb786.png) . Aby rozwiązać zadanie w wersji basic wystarczyło tylko uwierzyć w prawdziwość tego stwierdzenia. Ale oczywiście lepiej było od razu je udowodnić, tym bardziej, że jest to dość łatwe: zakładając, że umiemy w ten sposób przedstawić
. Aby rozwiązać zadanie w wersji basic wystarczyło tylko uwierzyć w prawdziwość tego stwierdzenia. Ale oczywiście lepiej było od razu je udowodnić, tym bardziej, że jest to dość łatwe: zakładając, że umiemy w ten sposób przedstawić 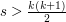 , zawsze możemy zmniejszyć jeden z elementów tej reprezentacji aby uzyskać rozkład
, zawsze możemy zmniejszyć jeden z elementów tej reprezentacji aby uzyskać rozkład 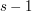 . Równie łatwo znaleźć rozkład danego
. Równie łatwo znaleźć rozkład danego  : jeśli
: jeśli 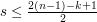 zmniejszamy
zmniejszamy  o jeden, a w przeciwnym wypadku bierzemy
o jeden, a w przeciwnym wypadku bierzemy  , zmniejszamy
, zmniejszamy  o
o  , a
, a  o jeden.
o jeden.
Uważny Czytelnik może dostrzec w (odpowiednio mocno powiększonym, w zależności od wady wzroku) logo zawodów kod rozwiązania do wersji basic.


 jako sumy k {\bf różnych} liczb naturalnych z przedziału
jako sumy k {\bf różnych} liczb naturalnych z przedziału ![$ [1,n] $](/files/tex/22cbb292a9943b8e56b2b467a0dddbe0f5afb786.png) . Zacznijmy od dwóch prostych spostrzeżeń:
. Zacznijmy od dwóch prostych spostrzeżeń:
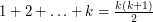 ,
,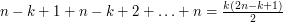 .
.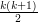 a
a 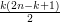 da się przedstawić jako sumę
da się przedstawić jako sumę  różnych liczb z przedziału
różnych liczb z przedziału 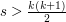 , zawsze możemy zmniejszyć jeden z elementów tej reprezentacji aby uzyskać rozkład
, zawsze możemy zmniejszyć jeden z elementów tej reprezentacji aby uzyskać rozkład 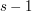 . Równie łatwo znaleźć rozkład danego
. Równie łatwo znaleźć rozkład danego 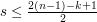 zmniejszamy
zmniejszamy  o jeden, a w przeciwnym wypadku bierzemy
o jeden, a w przeciwnym wypadku bierzemy 

