Referendum w sprawie obliczeń wielopodmiotowych
26.12.2010 - Agata Murawska
   
Przy prawie każdych wyborach odbywających się w ciągu ostatnich kilku lat wspominało się coraz głośniej potrzebę umożliwienia głosowania drogą elektroniczną. Zagadnienie to wzbudza wiele kontrowersji od kilkudziesięciu lat, nie będziemy więc rozważać wszystkich możliwych za i przeciw różnych proponowanych modeli, w jakich można takie wybory przeprowadzić. W idealnym świecie istnieje zaufana “strona trzecia”, której możemy powierzyć obliczenie sumy. Każdy przedstawia swój głos, a następnie mąż zaufania liczy sumę głosów na “TAK”. W stosowanym w Polsce systemie udziału w referendum, karteczka, którą wrzucamy do urny nie jest podpisana, a wszystkie kartki są mieszane, zanim zostaną policzone. Zapewnia to potrzebną nam anonimowość. Jak zasymulować takie zabezpieczenie przy głosowaniu elektronicznym? Obliczenia jakie?!
Określenie “obliczenia wielopodmiotowe” może brzmieć jak zaawansowana chińszczyzna dla tych, którzy nie mieli jeszcze styczności z poprzednim artykułem na ten temat - “Kto jest najbogatszy i czy to naprawdę miłość?”. ..więc jak to policzyć?Okazuje się, że istnieje uniwersalne rozwiązanie dla tego typu problemów. Zapewne zetknęliście się już z pojęciem bramka logiczna. Będzie ono intensywnie używane w poniższym rozwiązaniu, zatem przypomnijmy.. Bramka logiczna to, w ogólnym przypadku, podstawowa “cegiełka” w konstrukcji układu scalonego, która wykonuje proste obliczenie. Istnieje wiele rodzajów bramek, wykonujących różne operacje logiczne, ale nas interesują tylko dwie - bramka AND oraz bramka NOT.
To, co jest z naszej perspektywy najważniejszą cechą bramek logicznych to fakt, że przy ich pomocy da się zasymulować każdą funkcję. Ćwiczenie Spróbuj przy pomocy bramek logicznych skonstruować układ, który dodaje dwie liczby dwubitowe. RozwiązanieOmówienie możliwości bramek logicznych to w zasadzie materiał na osobny artykuł, musimy zatem uwierzyć na słowo, że w tych maleństwach drzemią ogromne możliwości - to znaczy każde obliczenie, jakie przyjdzie nam do głowy, da się zrealizować za pomocą (odpowiednio dużej) ilości bramek AND oraz NOT. Jak?
(1 ocena) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


 -osobowej grupie ludzi.
-osobowej grupie ludzi. 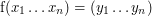 , przy czym każdy z
, przy czym każdy z 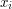 i nie chce swojej części udostępnić pozostałym uczestnikom protokołu. Również wynik obliczenia ma być podzielony tak, że każdy zna tylko swój udział - często jednak rezygnuje się z tej ostatniej własności, uznając wynik obliczeń za wspólny dla wszystkich uczestników.
i nie chce swojej części udostępnić pozostałym uczestnikom protokołu. Również wynik obliczenia ma być podzielony tak, że każdy zna tylko swój udział - często jednak rezygnuje się z tej ostatniej własności, uznając wynik obliczeń za wspólny dla wszystkich uczestników.
 i
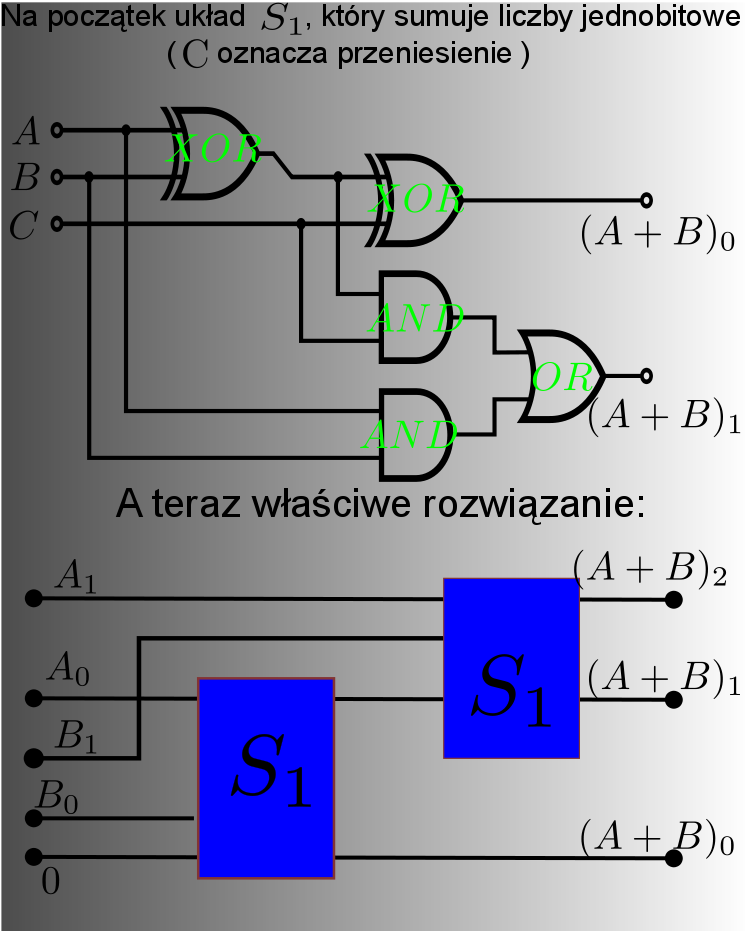
i  , a zwracająca ich koniunkcję -
, a zwracająca ich koniunkcję - 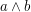
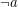
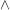 i
i  ), obliczyć ją przy pomocy MPC
), obliczyć ją przy pomocy MPC


